All GMAT Math Resources
Example Questions
Example Question #101 : Quadrilaterals
Calculate the length of the diagonal for a rectangle with a length of 

The diagonal of a rectangle can be thought of as the hypotenuse of a right triangle whose base and height are the length and width of the rectangle, respectively. This means we can use the Pythagorean Theorem to calculate the length of the diagonal for a rectangle:
Example Question #2 : Calculating The Length Of The Diagonal Of A Quadrilateral
Rhombus 




None of the other choices gives a correct answer.
The area of a rhombus is half the product of the lengths of its diagonals, which here are 

Since both diagonals have whole numbers as their lengths, and 


The quotient is
Since we can multiply both sides by 

we know that

so we can eliminate 12 and 16.
Also, since 

If 


Example Question #211 : Geometry
Rhombus 


A rhombus has four sides of equal length. Since Rhombus 





Example Question #1 : Calculating The Length Of The Diagonal Of A Quadrilateral
Rhombus 
Which of the following could be true about the values of 

None of the other responses gives a correct answer.
The area of a rhombus is half the product of the lengths of its diagonals, which here are 

Therefore, we need to test each of the choices to find the pair of diagonal lengths for which this holds.

Area:
Area:
Area:
Area:

Example Question #51 : Rhombuses
Rhombus 


The sides of a rhombus are all congruent; since the perimeter of Rhombus 
The referenced rhombus, along with diagonal 

Since consecutive angles of a rhombus, as with any other parallelogram, are supplementary, 






Example Question #51 : Rhombuses
Rhombus 


The referenced rhombus, along with diagonals 

The four sides of a rhombus have equal measure, so each side has measure one fourth of the perimeter of 48, which is 12.
Since consecutive angles of a rhombus, as with any other parallelogram, are suplementary, 








and

Since the diagonals of a rhombus bisect each other, 
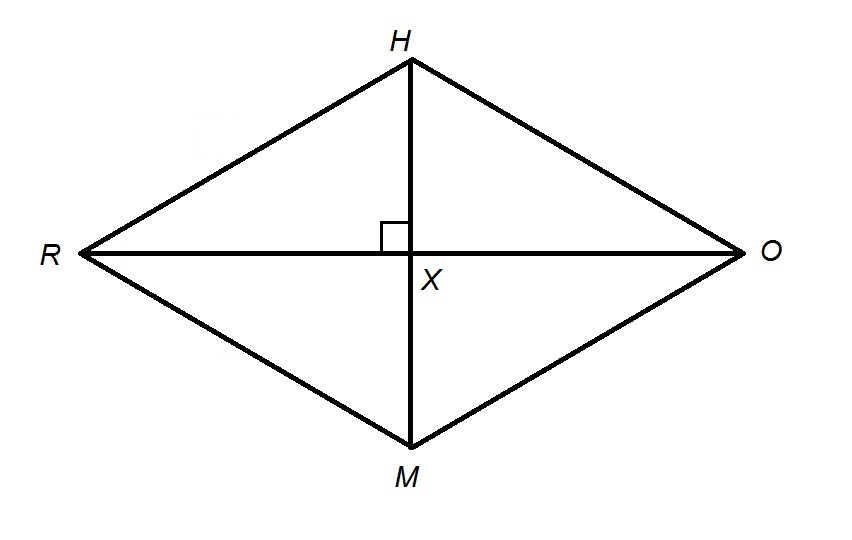
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
Given: Quadrilateral 





Give the length of diagonal 
None of the other responses is correct.
The Quadrilateral 


. We call the point of intersection 

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, 







By the 30-60-90 Theorem, since 


By the 45-45-90 Theorem, since 


The diagonal 

Example Question #1 : Calculating Whether Quadrilaterals Are Similar
Which of the following rectangles is similar to one with a length of 

In order for two rectangles to be similar, the ratio of their dimensions must be equal. We can check which dimensions are those of a rectangle similar to the given one by first calculating the ratio of the length to the width for the given rectangle, and then doing the same for each of the answer choices until we find which has an equal ratio between its dimensions:
So in order for a rectangle to be similar to the given rectangle, this must be the ratio of its length to its width. Now we check the answer choices, in no particular order, for one with this ratio:
We can see that only the rectangle with a length of 

Example Question #2 : Calculating Whether Quadrilaterals Are Similar
Which of the following dimensions would a rectangle need to have in order to be similar to one with a length of 

In order for two rectangles to be similar, the ratio of their dimensions must be equal. We can calculate the ratio of length to width for the given rectangle, and then check the answer choices for the rectangle whose dimensions have the same ratio:
Now we check the answer choices, in no particular order, and the dimensions with the same ratio are those of the rectangle that is similar:
We can see that a rectangle with a length of 

Example Question #221 : Geometry

Refer to the above Trapezoid 

Trapezoid 


Give the length of 
The length of the midsegment of a trapezoid - the segment that has as its endpoints the midpoints of its legs - is half the sum of the lengths of its legs. Therefore, Trapezoid 

Sidelengths of similar figures are in proportion. If the similarity ratio is 




meaning that the ratio of the lengths of the midsegments will be the same as the similarity ratio. Since the length of the midsegment of Trapezoid 

The ratio of the length of 


All GMAT Math Resources
















































































