GED Math : Statistics
Study concepts, example questions & explanations for GED Math
All GED Math Resources
Example Questions
Example Question #211 : Statistics
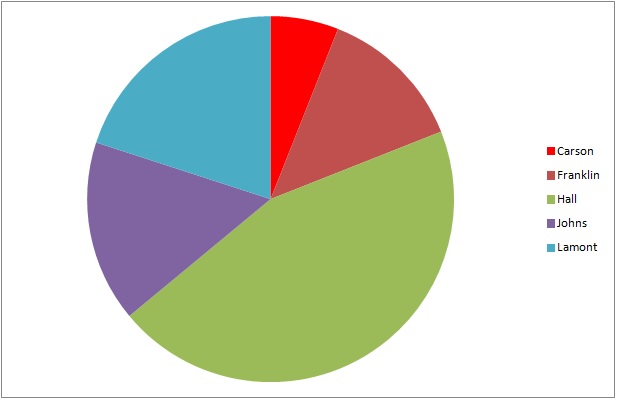
The above graph represents the results of a general election for two seats on the city council of Wilson City. Frankllin and Hall are Democrats; Johns and Lamont are Republicans; Carson is an independent.
4,987 people voted for Republicans. Which of the following is the best estimate of the number of people who voted in the election overall?
The two wedges that represent the Republican candidates - purple (Johns) and blue (Lamont) - make up about 40% of the circle. The problem becomes, essentially, to figure out what 4,987 is 40% of. This can be done by dividing 4,987 by 0.40:
12,500 is the best estimate.
Example Question #3 : Pie Charts
The above graph represents the results of a general election for two seats on the city council of Lincoln City. Frankllin and Hall are Democrats; Johns and Lamont are Republicans; Carson is an independent.
4,429 people voted for Democrats. Which of the following is the best estimate for the number of people who voted for Republicans?
The two wedges that represent the Democratic candidates - green (Hall) and dark red (Franklin) - together make up about 55% of the circle. The two wedges that represent the Republican candidates - purple (Johns) and blue (Lamont) - make up about 40% of the circle. We can estimate the number of people who voted for a Republican using a proportion statement:
Solve for 
The best estimate is 3,200 votes.
Example Question #211 : Statistics
Refer to the above graph. How many people voted against Vickers?
Do not use a calculator.
Add the number of people who voted for each of the other four candidates:
Example Question #212 : Statistics
Refer to the above graph. Which of the following comes closest to the ratio of people who voted for Zimmerman to people who voted for Ullman?
Divide the number of people who voted for Zimmerman, 512, by the number of people who voted for Ullman, 133.
About four times as many people voted for Zimmerman as Ullman, so of the given choices, 
Example Question #2 : Pie Charts
The above circle graph shows the results of a student body election. By the rules, if no candidate wins more than 50% of the vote, there will be a runoff between the top two finishers.
Which of the following questions cannot be answered about the election by examining the above graph?
How many more votes did Williams get than Vickers?
What percent of the vote did Ullman win?
How many students did not vote?
Who will face each other in the runoff?
How many students did not vote?
Ullman's percent of the vote can be calculated by dividing 133 by the sum of the voters of the five candidates. Vickers' number can be subtracted from Willams' number to determine the difference. The two participants in the runoff can be easily seen to be Zimmerman and Williams as they won the most and second-most votes.
However, the question "How many students did not vote?" cannot be answered as the graph only shows the students who did.
Example Question #7 : Pie Charts
Do NOT use a calculator for this question.
Refer to the above circle graph.
The top two finishers engage in a runoff election.
The third-place finisher tells his voters to choose the second-place finisher. The fourth- and fifth-place finishers tell their voters to choose the first-place finisher.
If each voter who selected one of the top two finishers stays with his choice, and every other voter does what is requested of him by his original chosen candidate, who will win the election?
Williams
Zimmerman
Vickers
Ullman
Williams
In one group will be those who voted for first-place finisher Zimmerman, fourth-place finisher Ullman, and fifth-place finisher Young. These people will vote for Zimmerman.
In the second group will be those who voted for second-place finisher Williams and third-place finisher Vickers. These people will vote for Williams.
The pieces of the circle representing Vickers and Williams together make up more than half the circle. Therefore, Williams will win the runoff.
Example Question #212 : Statistics
Refer to the above circle graph.
To the nearest whole percent, what percent of the students voted for the most popular candidate?
The highest vote-getter was Zimmerman, who got 512 votes; this is the part. The whole is the number of persons who voted, which is the sum:
The percent can be found by calculating:
Example Question #212 : Statistics
Refer to the above graph. Which of the following comes closest to the ratio of people who voted against Williams to people who voted for Williams?
The number of people who voted for candidates other than Williams is
433 people voted for Williams.
Divide 1,091 by 433:
About 2.5, or 
Example Question #213 : Statistics
Refer to the above graph. To the nearest whole number, what percent of the people voted against Ullman?
The whole is the number of persons who voted, which is the sum:
The part is the number of people who voted for candidates other than Ullman, which is
We now want to know what percent of 1,524 is 1,391, which can be answered by calculating:
Example Question #11 : Pie Charts
The above graph represents the results of a general election for mayor of Washington City. Hall is a Republican; Johns is a Democrat; the other three are independents.
5,328 people voted for Hall. Which is the best estimate for the number of people who voted for an independent candidate?
The green wedge, which represents Hall, is about 45% of the circle. The three wedges representing independents Carson, Franklin, and Lamont - dark red, bright red, and turquoise, respectively - together comprise about 40% of the circle. We can set up, and solve for the unknown in a proportion statement as follows:
4,700 is the best estimate.
All GED Math Resources
