All GED Math Resources
Example Questions
Example Question #81 : Squares, Rectangles, And Parallelograms
Square 1 has area 16; Square 2 has perimeter 16.
Which square has the longest sides?
The information is insufficient.
Square 1
Neither
Square 2
Neither
The length of a side of a square is equal to the square root of its area. Square 1 has area 16, so each side has length 
The length of a side of a square is one fourth its perimeter. Square 2 has perimeter 16, so each side has length 
The squares are of equal size, so the correct response is "neither".
Example Question #382 : 2 Dimensional Geometry
Your mother made a casserole in a pan whose length is 9 inches and whose width is one and a half times the length. What is the area of the casserole pan?
To find the area, you need to multiply the dimensions. First, however, we need to find our width.
We can find our width by using the clue: "...one and a half times the length"
So, do the following:
Next, perform the following operation:
Making our answer:
Example Question #91 : Squares, Rectangles, And Parallelograms
In the figure below, if the minor arc 


Recall the relationship between a central angle and the length of the arc that it intercepts.
Since the radius of the circle is given, we can find its circumference.
For the given circle,
We can plug in all the given information and solve for the central angle then.
Example Question #42 : Area Of A Quadrilateral
If a rectangular television has a diagonal of 


Drawing out the rectangle in question shows that we can use the Pythagorean Theorem to find the width of the rectangle.
Now, recall how to find the area of a rectangle:
Plug in the width and height of the rectangle to find the area.
Example Question #91 : Squares, Rectangles, And Parallelograms
A square and a circle share a center as shown by the figure below.

If the length of a side of the square is 
In order to find the area of the shaded region, we will need to find the area of the circle then subtract the area of the square from it.
Start by finding the area of the square. Since we know the side length of the square, we can write the following:
Next, we find the area of the circle. Since the question states that the length of a side of the square is half the radius of the circle, the radius of the circle must be 
Now, subtract these two values to find the area of the shaded region.
Example Question #91 : Squares, Rectangles, And Parallelograms
If the area of square is 

Figuring out the perimeter of a square from this information is luckily pretty easy. Since the sides of a square are all the same size, you know also that 
Taking the square root of both sides, you get:
Now, the perimeter of the square is just 

Example Question #51 : Area Of A Quadrilateral
If the perimeter of a square is 
Since the four sides of a square are equal, you know that the perimeter of a square is defined as:
For our data, this is:
Solving for 
Now, the area of a square is just:



Example Question #381 : 2 Dimensional Geometry
In Rhombus 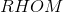








The figure referenced is below.

The sides of a rhombus are congruent by definition, so 

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so





The correct response is that 
Example Question #92 : Squares, Rectangles, And Parallelograms
Given Quadrilateral 
I) 
II) 
III) 



Statement I only
Statement II only
Statement I, II, or III
Statement III only
Statement II only
Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Example Question #3 : Angles And Quadrilaterals
You are given Parallelogram 


I)
II)
III)
Statement II only
Statement I only
Statement I, II, or III
Statement III only
Statement I, II, or III
A rectangle is defined as a parallelogram with four right, or 
Since opposite angles of a paralellogram are congruent, if one angle measures 



In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
Certified Tutor
Certified Tutor
All GED Math Resources
























































