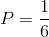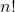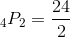All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #91 : Conditional Probability & The Rules Of Probability
The probability of winning a certain carnival game is 
.08
.01
.13
.7
.8
.13
Example Question #92 : Conditional Probability & The Rules Of Probability
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of four hormones: auxin, gibberellin, abscisic acid, and cytokinin. The researcher can only give each sprout a combination of three hormones and the order in which they are given matters for the study. How many outcomes are present in this study?
Cannot be determined
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing four items or things—in this case the hormones: auxin, gibberellin, abscisic acid, and cytokinin. Next, we know that there we can have three hormones in each treatment or three slots. Last, the order of the hormones matters to the researcher. Given this information we must use the permutation formula.
Substitute in our known values.
Expand the factorials and solve.
There are twenty-four possible outcomes.
Example Question #1 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of four hormones: auxin, gibberellin, abscisic acid, ethylene, and cytokinin. The researcher can only give each sprout a combination of four hormones and the order in which they are given does not matter for this particular study. How many outcomes are present in this study?
Cannot be determined
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing five items or things—in this case the hormones: auxin, gibberellin, abscisic acid, ethylene, and cytokinin. Next, we know that there can be four hormones in each treatment or four slots/bins. Last, the order of the hormones does not matter to the researcher. Given this information we must use the combination formula.
Substitute in our known values.
Let's start by expanding the factorials.
Simplify.
There are five outcomes.
Example Question #4 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of nine different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of eight hormones and the order in which they are given matters for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing four items or things—in this case the hormones: auxin, gibberellin, abscisic acid, and cytokinin. Next, we know that there we can have three hormones in each treatment or three slots. Last, the order of the hormones matters to the researcher. Given this information we must use the permutation formula.
Substitute in our known values.
Expand the factorials and solve.
Example Question #5 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of seven different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of six hormones and the order in which they are given matters for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing four items or things—in this case the hormones: auxin, gibberellin, abscisic acid, and cytokinin. Next, we know that there we can have three hormones in each treatment or three slots. Last, the order of the hormones matters to the researcher. Given this information we must use the permutation formula.
Substitute in our known values.
Expand the factorials and solve.
Example Question #101 : Conditional Probability & The Rules Of Probability
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of eleven different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of ten hormones and the order in which they are given does not matter for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing five items or things—in this case the hormones: auxin, gibberellin, abscisic acid, ethylene, and cytokinin. Next, we know that there can be four hormones in each treatment or four slots/bins. Last, the order of the hormones does not matter to the researcher. Given this information we must use the combination formula.
Substitute in our known values.
Expand the factorials and solve.
Example Question #102 : Conditional Probability & The Rules Of Probability
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of twelve different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of eleven hormones and the order in which they are given does not matter for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing five items or things—in this case the hormones: auxin, gibberellin, abscisic acid, ethylene, and cytokinin. Next, we know that there can be four hormones in each treatment or four slots/bins. Last, the order of the hormones does not matter to the researcher. Given this information we must use the combination formula.
Substitute in our known values.
Expand the factorials and solve.

Example Question #8 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of thirteen different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of twelve hormones and the order in which they are given does not matter for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing five items or things—in this case the hormones: auxin, gibberellin, abscisic acid, ethylene, and cytokinin. Next, we know that there can be four hormones in each treatment or four slots/bins. Last, the order of the hormones does not matter to the researcher. Given this information we must use the combination formula.
Substitute in our known values.
Expand the factorials and solve.
Example Question #9 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of eight different hormones (e.g auxin, gibberellin, abscisic acid, and cytokinin, etc.). The researcher can only give each sprout a combination of seven hormones and the order in which they are given matters for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing four items or things—in this case the hormones: auxin, gibberellin, abscisic acid, and cytokinin. Next, we know that there we can have three hormones in each treatment or three slots. Last, the order of the hormones matters to the researcher. Given this information we must use the permutation formula.
Substitute in our known values.
Expand the factorials and solve.
Example Question #10 : Permutations And Combinations Of Compound Events: Ccss.Math.Content.Hss Cp.B.9
A researcher is studying the effects of hormone treatments on coleoptile and radicle growth in corn sprouts. The researcher wants to test the effects of five different hormones (e.g. auxin, gibberellin, abscisic acid, cytokinin, etc.). The researcher can only give each sprout a combination of four hormones and the order in which they are given matters for the study. How many outcomes are present in this study?
In order to solve this problem, we need to discuss probabilities, permutations, and combinations. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
But what happens if we do not know how many outcomes we have (e.g. in the question presented in the problem)? Outcomes are not always easily identified or calculated; however, mathematical operations associated with permutations and combinations can make these processes easier. Permutations provide the number of outcomes when the order of events matter. Permutations are calculated using the following formula:
In this formula, the variable, 

Now, we need to calculate the number of permutations present in this model; however, we need to understand how to perform calculations involving factorials. Factorials are denoted with an exclamation point (!). For example, let's observe the following operation:
This denotes that for every non-negative integer, 

Let's use this information to solve our marble example.
Solve.
Simplify.
We know that there are twelve possible permutations. We can write them in the following table:

Next, we need to discuss combinations. Combinations help us to calculate the number of outcomes in a given model when order does not matter. In other words, pulling a red and a blue marble is the same as pulling a blue and red marble. Combinations are calculated using the following formula:
The combination formula is similar to the permutation formula. In the combination formula the variable, 

Let's start by expanding the factorials.
Simplify.
Notice that the only difference between this and the permutation formula is that we have an additional term on the denominator where we have the factorial of the number of bins or slots multiplied by the factorial of the number of things minus the number of slots. We know that there are six different combinations of outcomes for this model. We can write them out in the following table:

Now, let's use this information to solve the given problem. We know that the researcher is testing four items or things—in this case the hormones: auxin, gibberellin, abscisic acid, and cytokinin. Next, we know that there we can have three hormones in each treatment or three slots. Last, the order of the hormones matters to the researcher. Given this information we must use the permutation formula.
Substitute in our known values.
Expand the factorials and solve.
All Common Core: High School - Statistics and Probability Resources