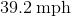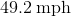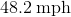All Common Core: High School - Number and Quantity Resources
Example Questions
Example Question #121 : High School: Number And Quantity
Bob is cruising south down a river at 

Not possible to find
In order to figure this out, we need to create a picture.


Since bob is traveling south, and the current is traveling west, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #2 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Amanda is cruising north down a river at 

In order to figure this out, we need to create a picture.

Since Amanda is traveling north, and the current is traveling east, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #3 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Jack slides down a hill at 

Since the rock is going in the opposite direction of Jack, we simply subtract the speed of the rock from how fast Jack is going down the hill.
Example Question #4 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
If an airplane is flying south at 

In order to figure this out, we need to create a picture.

Since the airplane is traveling south, and the wind is coming from the west, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #122 : High School: Number And Quantity
Jill slides down a hill at 


Since the coin is going in the same direction as Jill, we simply add the speed of the coin and how fast Jill is going down the hill.
Example Question #6 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Bob slides down a hill at 

Since Bob's wallet is going in the opposite direction, we simply subtract the speed of the wallet from how fast Bob is going down the hill.
Example Question #1 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
John is cruising north down a river at 

In order to figure this out, we need to create a picture.

Since John is traveling north, and the current is traveling east, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #2 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Jack slides down a hill at 

Since the rock is going in the same direction as Jack, we simply add the speed of the rock to how fast Jack is going down the hill.
Example Question #3 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
If an airplane is flying south at 

Since the airplane and the wind are going in opposite directions, we simply subtract the speed of the wind from the speed of the plane.
Example Question #4 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
If an airplane is flying south at 

Since the airplane and the winds are going the same direction, we simply add the airplane and wind speeds together.
Certified Tutor
Certified Tutor
All Common Core: High School - Number and Quantity Resources