In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.

First, we can subtract  from both sides:

This equation is in slope-intercept form; thus,  is the correct answer. 

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.

First, we can subtract  from both sides:

Next, we can divide each side by 

This equation is in slope-intercept form; thus,  is the correct answer. 

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.

First, we can subtract  from both sides:

This equation is in slope-intercept form; thus,  is the correct answer.

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

This equation is in slope-intercept form; thus,  is the correct answer. 

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.

First, we can subtract  from both sides:

This equation is in slope-intercept form; thus,  is the correct answer. 

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

This equation is in slope-intercept form; thus,  is the correct answer. 

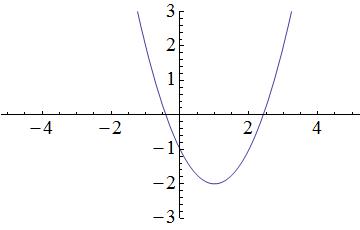
Start by visualizing the graph associated with the function :

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of  looks like this:

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function  :

In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear. 

Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form. 

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the  value is to the second power. 

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.

First, we can subtract  from both sides:

Next, we can divide each side by 

This equation is in slope-intercept form; thus,  is the correct answer.