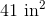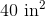Common Core: 7th Grade Math : Solve for area of a rectangle
Study concepts, example questions & explanations for Common Core: 7th Grade Math
All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Solve For Area Of A Rectangle
Calculate the area of the provided figure.
In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #2 : Solve For Area Of A Rectangle
Calculate the area of the provided figure.
In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve For Area Of A Rectangle
In rectangle ABCD, the perimeter is 48 and side BC measures 4. What is the area of rectangle ABCD?
48
88
80
72
64
80
The perimeter of a rectangle is 2L + 2W, or 2 times the length plus 2 times the width. Here you're given that side BC is 4, which means that the opposite side, AD, is also 4. So since that is two widths, you now have:
8 + 2L = 48
So 2L = 40
That means that the length is 20.
Since the area is LW, you can calculate the area as 20 * 4 = 80.
Example Question #4 : Solve For Area Of A Rectangle
What is the area of rectangle WXYZ?
100
125
50
150
120
150
The area of a triangle is Length times Width. Here you can see that the length is 15 and the width is 10, so when you multiply 15 * 10 the answer is 150.
Example Question #1 : Solve For Area Of A Rectangle
A rectangle's length is twice as long as its width. If the width of the rectangle is 4, what is its area?
32
16
24
12
8
32
The area of a rectangle is Length * Width. Here you're given the width as 4, so all you need to do is find the length and you can apply the formula.
Since the width is 4 and you know that the length is twice as long, that makes the length 8. Then Length * Width would be 8 * 4 = 32.
Example Question #6 : Solve For Area Of A Rectangle
A rectangle has sides of 2, 2, 7, and 7. What is the area of that rectangle?
14
7.5
9
22
18
14
The area of a triangle is Length * Width, and in a rectangle opposite sides are parallel and have the same length. So here you know that the widths are 2 and the lengths are 7. So multiply 7 * 2 to get your answer, which is 14.
All Common Core: 7th Grade Math Resources
