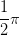Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 7th Grade Math : Grade 7

Study concepts, example questions & explanations for Common Core: 7th Grade Math

Create An Account

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #26 : Area Of A Circle

What is the area of the circle provided?

Possible Answers:

$19\pi\textup{ in}^2$

$18\pi\textup{ in}^2$

$15\pi\textup{ in}^2$

$16\pi\textup{ in}^2$

$17\pi\textup{ in}^2$

Correct answer:

$16\pi\textup{ in}^2$

Explanation:

In order to solve this problem, we need to recall the formula for the area of a circle:

$A= r^2\pi$

The circle in this question provides us with the diameter, so we first have to solve for the radius. Remember, the radius is half the diameter:

$r=\frac{d}{2}$

$r=\frac{8}{2}$

r=4

Now that we have the radius we can use the formula to solve:

$A=4^2\pi$

Solve:

$A=16\pi\textup{ in}^2$

Report an Error

Example Question #1 : Circumference Of A Circle

What is the circumference of a circle with a radius equal to ?

Possible Answers:

$196\pi$

$14\pi$

$7\pi$

$49\pi$

Correct answer:

$14\pi$

Explanation:

The circumference can be solved using the following equation:

$C=2r\pi=2(7)\pi=14\pi$

Report an Error

Example Question #1 : Circumference Of A Circle

The radius of a circle is t^2 . Give the circumference of the circle in terms of .

Possible Answers:

$2\pi t^2$

$\pi t$

$4\pi t^2$

$\pi t^2$

$2\pi t$

Correct answer:

$2\pi t^2$

Explanation:

The circumference can be calculated as $Circumference =2\pi r$ , where is the radius of the circle.

$Circumference =2\pi r=2\pi t^2$

Report an Error

Example Question #2 : Circumference Of A Circle

What is the circumference of a circle with a radius of ?

Possible Answers:

$16\pi$

$16\pi^{2}$

$28\pi$

$8\pi$

Correct answer:

$16\pi$

Explanation:

The circumference can be solved using the following equation:

$C=2r\pi$

Where represents the radius. Therefore, when we substitute our radius in we get:

$=2(8)\pi =16\pi$

Report an Error

Example Question #1 : How To Find Circumference

If this circle has a diameter of 12 inches, what is its circumference?

Circle_12d

Possible Answers:

$12\pi\ \text{inches}$

$44\ \text{inches}$

$38\ \text{inches}$

$6\pi\ \text{inches}$

none of these

Correct answer:

$12\pi\ \text{inches}$

Explanation:

Know that the formula for circumference is $C=D\pi$ , where C is the circumference and D is the diameter. It is given that the diameter is 12 inches. Therefore, the circumference is $C=12\pi \hspace\ \text{inches}$

Report an Error

Example Question #1 : Circumference Of A Circle

If a circle has an area of $81\pi$ , what is the circumference of the circle?

Possible Answers:

$27\pi$

$90\pi$

$18\pi$

$81\pi$

$9\pi$

Correct answer:

$18\pi$

Explanation:

The formula for the area of a circle is πr². For this particular circle, the area is 81π, so 81π = πr². Divide both sides by π and we are left with r²=81. Take the square root of both sides to find r=9. The formula for the circumference of the circle is 2πr = 2π(9) = 18π. The correct answer is 18π.

Report an Error

Example Question #2 : Circumference Of A Circle

If a circle has an area of $16\pi \; in^{2}$ , what is the circumference?

Possible Answers:

$10\pi \; in$

$12\pi \; in$

$4\pi \; in$

$6\pi \; in$

$8\pi \; in$

Correct answer:

$8\pi \; in$

Explanation:

For a circle, the formula for area is $A = \pi r^{2}$ and the formula for circumference is $C=\pi d$ , where is the radius and is the diameter.

Plug the known quantities into the area formula and solve for the radius:

$16\pi =\pi r^{2}$

$r=4\; in$

Now plug this value into the circumference formula to solve:

$C = \pi d = \pi 2r = \pi 2(4) = 8\pi\; in$

Report an Error

Example Question #2 : Circumference Of A Circle

Find the circumference of a circle with a radius of .

Possible Answers:

$4\pi$

$\pi$

$2\pi$

$6\pi$

Correct answer:

$4\pi$

Explanation:

Recall the formula for finding the circumference of a circle:

$\text{Circumference}=2\times\text{radius}\times\pi$

We can substitute in the value for the radius in order to find the circumference of the circle in question.

$\text{Circumference}=2\times 2 \times\pi$

Solve.

$\text{Circumference}=4\times \pi$

Simplify.

$\text{Circumference}=4\pi$

Report an Error

Example Question #5 : Circumference Of A Circle

Find the circumference of a circle that has a radius of $\frac{1}{2}$ .

Possible Answers:

$\frac{1}{2}\pi$

$\pi$

$2\pi$

$-\pi$

Correct answer:

$\pi$

Explanation:

Recall the formula for finding the circumference of a circle:

$\text{Circumference}=2\times\text{radius}\times\pi$

We can substitute in the value for the radius in order to find the circumference of the circle in question.

$\text{Circumference}=2\times \frac{1}{2} \times\pi$

Solve.

$\text{Circumference}=\frac{2}{2} \times\pi$

Simplify.

$\text{Circumference}= \pi$

Report an Error

Example Question #3 : Circumference Of A Circle

Find the circumference of the circle with a radius of .

Possible Answers:

$5\pi$

$100\pi$

$20\pi$

$10\pi$

Correct answer:

$20\pi$

Explanation:

Recall the formula for finding the circumference of a circle:

$\text{Circumference}=2\times\text{radius}\times\pi$

We can substitute in the value for the radius in order to find the circumference of the circle in question.

$\text{Circumference}=2\times 10 \times\pi$

Solve.

$\text{Circumference}=20\times\pi$

Simplify.

$\text{Circumference}=20\pi$

Report an Error

View Tutors

Clinton
Certified Tutor

Rensselaer Polytechnic Institute, Current Undergrad, Biology, General. Albany Medical College, PHD, Molecular and Cellular Ph...

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Los Angeles, English Tutors in Atlanta, English Tutors in New York City, ISEE Tutors in San Francisco-Bay Area, Reading Tutors in San Diego, Calculus Tutors in San Diego, Computer Science Tutors in Phoenix, Reading Tutors in Phoenix, ISEE Tutors in Chicago, Biology Tutors in Washington DC

Popular Courses & Classes

LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in New York City, GRE Courses & Classes in Seattle, ACT Courses & Classes in Seattle, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in New York City, GMAT Courses & Classes in Houston, GMAT Courses & Classes in Miami, Spanish Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Miami, ACT Test Prep in Seattle, ISEE Test Prep in Los Angeles, GRE Test Prep in Dallas Fort Worth, ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Phoenix, ISEE Test Prep in Denver, GRE Test Prep in Los Angeles, GMAT Test Prep in Atlanta, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 7th Grade Math : Grade 7

Study concepts, example questions & explanations for Common Core: 7th Grade Math

All Common Core: 7th Grade Math Resources

Example Questions

Example Question #26 : Area Of A Circle

Example Question #1 : Circumference Of A Circle

Example Question #1 : Circumference Of A Circle

Example Question #2 : Circumference Of A Circle

Example Question #1 : How To Find Circumference

Example Question #1 : Circumference Of A Circle

Example Question #2 : Circumference Of A Circle

Example Question #2 : Circumference Of A Circle

Example Question #5 : Circumference Of A Circle

Example Question #3 : Circumference Of A Circle

All Common Core: 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: