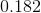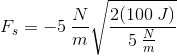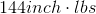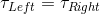All College Physics Resources
Example Questions
Example Question #1 : Universal Gravitation
The gravitational force between two objects is 
So the fact that we don't actually know any of the numbers doesn't matter.
What matters is we have the equation
The masses have a direct proportional relationship with the force. That means that if a mass doubles, the force doubles.
We can also see that the radius (distance between the masses) has an inverse square relationship with Force. So if we double the radius, we divide the force by 4.
So based on the problem, we triple a mass and double the radius. So we triple the force then divide by 4.
Example Question #1 : Tension
Suppose that an object of a certain mass that is hanging from a wall is suspended by two ropes. Which of the following gives an expression for the tension in each rope?
In this question, we're told that an object is hanging by being supported by two ropes. We're asked to find the tension in each rope.
When answering this question, we have to keep in mind all of the forces acting on the object. Since the object isn't moving, there is no net force acting on it. Moreover, we know that its weight acts downward while the tension in the ropes act upwards.
Example Question #2 : Tension
An object weighing 


For this question, we're told that an object hanging from a string is released from an initial height and allowed to swing. We're given the maximum velocity, the object's mass, and the length of the string. We're asked to find the maximum tension in the string.
The first step towards solving this problem is to realize that we're dealing with centripetal motion. When the object is released from an initial height, it begins to fall. But as it falls, the string exerts a tension on the mass and causes the mass to travel in a circular motion. Thus, the tension of the string is supplying the centripetal force.
Furthermore, it's important to remember the point at which the object will have maximum velocity. When the object was initially released from some initial height, all of the object's energy was in the form of gravitational potential energy. As it falls, that potential energy is converted into kinetic energy. Once the object reaches the very bottom of its path of motion, all of the potential energy it once had has been converted into kinetic energy at that instant. Since all of the energy is in the form of kinetic energy, and the object's mass remains constant, we know that this must be the point where the maximum velocity occurs.
Thus, we need to analyze the situation when the mass has swung to the very bottom of the path. At this point, the tension is providing an upward force. Moreover, the only downward force acting on the object is its weight due to gravity. The net force resulting from these two will result in the overall centripetal force on the object. We can put this into an equation as follows.
Since we're trying to solve for the tension in the string, we can isolate the 
Example Question #1 : Friction
Suppose a 


If the tension in the rope is 

To solve this problem, we first need to take into account the forces acting in the vertical direction separately from the forces acting in the horizontal direction.
First, let's start with the vertical direction. Here, the only force force acting downward is the weight of the box. There are two forces acting upwards on the box; one is the normal force and the other is the vertical component of the tension in the rope that is pulling the box. Because the box is not moving in the vertical direction, there is no net force. Thus, the sum of these forces is equal to zero.
Next, let's take a look at the forces acting horizontally on the box. Acting to the right of the box is the horizontal component of the tension in the rope. Acting to the left is the frictional force. Because the box is moving to the right, it must have experienced a net force in this direction. Thus, the sum of these horizontally acting forces will equal a net force.
Now, we can take the expression we obtained for the normal force and substitute it into the expression we obtained for the horizontally acting forces.
Now that we've found an expression for the coefficient of kinetic friction, all we need to do is plug in the values given in the question stem to arrive at the answer.
Example Question #1 : Using Free Body Diagrams
Which of these forces is identical to a normal force?
Force that is perpendicular to the surface
The scale weight of a body
The contact force
The perpendicular force
All of these
All of these
All of these are identical to a normal force.
Example Question #1 : Spring Force
A 



This questions requires an understanding of the conversion of gravitational potential energy to potential energy stored in the compression of a spring. The ball's initial potential energy is 









Example Question #1 : Spring Force
A block with mass 

The new equilibrium position will be where the spring force is opposite in direction and equal in magnitude to the gravitational force on the mass. This occurs where 



Example Question #1 : Spring Force
Supposed that an object attached to a spring with a spring constant of 
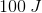
The first step in answering this question is to recognize that we're dealing with two components of a spring; force and energy. Hence, we'll need to utilize both equations. Because both of them share the term for the displacement of the object, that will be the variable that links the two expressions.
Having isolated the variable for displacement, we can plug this value into the force equation.
Now, we can plug in the values given to us in the question stem.
Note that the negative sign shown here indicates the direction of the force. This is because the force is acting in the direction opposite the displacement of the object. Since the question stem asks for the magnitude of force, we don't need to include the negative sign in our answer.
Example Question #1 : Torque
A mechanic is able to exert a maximum torque of 
The maximum amount of torque is the magnitude of the torque vector 



Example Question #1 : Torque
An object weighing 

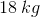
For this question, we'll need to take torque into account. The amount of torque caused by the object to the left of the fulcrum needs to be equal to the torque of the object to the right of the fulcrum.
Moreover, we can write out the equation for torque.
Combining these equations, we can set an expression for the torque on the left and the torque on the right.
Then we can set them equal to each other.
Next, we isolate the term for the distance on the right and we cancel out common units.
Finally, we plug in the values given in the question stem. Because we're told that both objects are sitting flat on the board, we know the force of their weight is perpendicular to the board, which gives a value of 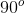
All College Physics Resources