All College Chemistry Resources
Example Questions
Example Question #2 : Le Chatelier's Principle
Consider the following equation at equilibrium:
What would happen if more 
There would be no change.
More 
More 
Less 
More 
Recall Le Chatelier's principle: A chemical system at equilibrium will shift in the direction that minimizes the disturbance to the system.
Before the addition of 

However, after the addition of 

In order to maintain equilibrium, the reaction will then shift right of favor the formation of more products.
Example Question #1 : Le Chatelier's Principle
Consider the following exothermic equation:
Which of the following actions will cause the products to be favored?
Increase the temperature at which the reaction is conducted.
Decrease the temperature at which the reaction is conducted.
Increase the amount of 
Decrease the amount of 
Decrease the temperature at which the reaction is conducted.
Since the equation is exothermic, you can think of heat as another product of the reaction:
Apply LeChatelier's principle to this equation.
If the temperature at which the reaction is decreased, that is akin to decreasing the amount of product made, thus causing the reaction to shift towards the products.
Example Question #1 : Common Ion Effect
Calculate the molar solubility of barium fluoride when it is dissolved in a solution containing 


Start by writing out the equation for the dissolution of barium fluoride.
Next, write out the chart to keep track of concentrations of each ion.
|
|
[ |
[ |
|
Initial |
0.00 |
0.200 |
|
Change |
+x |
+2x |
|
Equilibrium |
x |
0.200+2x |
In the chart, 


Now, write the equilibrium expression using the chemical equation:
Plug in the given 

At this point, use a graphing calculator to solve for 
The molar solubility of barium fluoride in sodium fluoride is 
Example Question #133 : College Chemistry
Suppose that a chemist wants to lower the concentration of calcium in an aqueous solution by precipitating it out, according to the following reaction expression.
Which of the following chemicals could the chemist add to the solution in order to precipitate the calcium?
Any of these
In this question, we're shown an equilibrium expression for a precipitation reaction in solution. We're asked to identify a compound that will help calcium precipitate out of solution.
To identify a compound that will precipitate calcium out of solution, we need to consider the equilibrium expression shown in the question stem. Applying Le Chatlier's principle, we'll need to consider the direction each of the answer choices will push the reaction in.
Adding 

Adding 
Adding 
Adding 


Example Question #1 : Solubility Product Constant
Express the solubility product constant expression for the given reaction.
The equilibrium given tells us how the solid dissolves in solution:
However, the solubility product constant (Ksp) given tells us the degree by which a solid dissolves in solution. The larger the Ksp, the more soluble a substance is in water. Writing this expression follows the same rules as other equilibrium constant expressions. Therefore solids and water (when it is the solvent) are omitted from this expression. You must raise the concentration of the substances involved to the power of its coefficient.
For the chemical reaction given, the Ksp is:
Example Question #2 : Solubility Product Constant
Express the solubility product constant expression for the given reaction.
The equilibrium given tells us how the solid dissolves in solution:
However, the solubility product constant (Ksp) given tells us the degree by which a solid dissolves in solution. The larger the Ksp, the more soluble a substance is in water. Writing this expression follows the same rules as other equilibrium constant expressions. Therefore solids and water (when it is the solvent) are omitted from this expression. You must raise the concentration of the substances involved to the power of its coefficient.
For the chemical reaction given, the Ksp is:
Example Question #1 : Solubility Product Constant
How many grams of 

To calculate how many grams of 
Using the dissociation equation
We can write out the equation for the solubility product constant as
Because there are 2 fluoride ions for every barium ion, we can rewrite the equation as
Now solve for x
Solve for the concentration of dissolved
Now that we have the concentration of dissolved 
Certified Tutor
Certified Tutor
All College Chemistry Resources




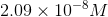




 ]
] ]
]![\text{K}_{sp}=[\text{Ba}^{2+}][\text{F}^-]^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/902868/gif.latex)








![K_{sp}=[Ca^{2+}][F^{-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986386/gif.latex)
![K_{sp}=\frac{[Ca^{2+}][F^{-}]^{2}}{[CaF_{2}]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986385/gif.latex)
![K_{sp}=[Ca^{2+}][F^{-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986384/gif.latex)
![K_{sp}=[Ca^{2+}][F^{-}]^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986383/gif.latex)

![K_{sp}=[Pb^{2+}][Cl^{-}]^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986388/gif.latex)
![K_{sp}=[Pb^{2+}][Cl^{-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986391/gif.latex)
![K_{sp}=[Pb^{2+}][Cl^{-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986389/gif.latex)
![K_{sp}=\frac{[Pb^{2+}][Cl^{-}]^{2}}{[PbCl_{2}]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/986390/gif.latex)








![\textrm{K}_{\textrm{sp}}=\textrm{[Ba}^{2+}][\textrm{F}^{\textrm{ -}}]^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995671/gif.latex)
![1.00\textrm{ x 10}^{-6}=\textrm{[Ba}^{2+}][\textrm{F}^{\textrm{ -}}]^{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995672/gif.latex)
![[\textrm{Ba}^{2+}]=x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995673/gif.latex)




![x=\sqrt[3]{2.50\textrm{ x 10}^{-7}}=6.30\textrm{ x 10}^{-3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995678/gif.latex)
![[\textrm{Ba}^{2+}]=6.30\textrm{ x 10}^{-3}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995679/gif.latex)

![[\textrm{BaF}_{2}]=[\textrm{Ba}^{2+}]=6.30\textrm{ x 10}^{-3}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/995680/gif.latex)




