All College Algebra Resources
Example Questions
Example Question #471 : College Algebra
Solve the following inequality.

To solve this inequality, we treat is a a regular equation. First, we add 8 to both sides.

We now divide both sides by 2 to get

Example Question #1 : Linear Inequalities
Solve:
To evaluate, we will need to multiply both sides by one-fifth.
The sign does not need to be switched unless we multiply or divide by a negative value.
The answer is:
Example Question #472 : College Algebra
Express the following linear inequality in interval notation.
Upon solving for x, we find that x is larger than -2. The left-hand term of the interval is -2 since it is the lower bound for our set, and it has a parenthesis around it because it is not included in our set (-2 is not greater than -2). The right-hand term of the interval is positive infinity because any number larger than -2 is in the set. There is always a parenthesis around infinity or negative infinity.
Example Question #481 : College Algebra
Express the following linear inequality in interval notation.
Upon solving for x, we find that x is less than or equal to 5. The left-hand term of the interval is negative infinity since any number less than 5 is in our set, and infinity always has a parenthesis around it. The right-hand term of the interval is 5 since it is the upper bound of our set. There is a bracket around it because 5 is included in our set (5 is less than or equal to 5).
Example Question #4 : Linear Inequalities
Express the following linear inequality in interval notation.
Upon expanding and solving for x, we find that x is greater than -1. The left-hand term of the interval is -1 since it is the lower bound of our set, and has a parenthesis around it because it is not in our set (-1 is not greater than -1). The right-hand term of the interval is infinity because any number larger than -1 is in our set, and there is always a parenthesis around infinity.
Example Question #5 : Linear Inequalities
Express the following linear inequality in interval notation.
Upon solving for x, we find that 8 is less than or equal to x which is less than or equal to 10, or x is greater than or equal to 8 AND x is less than or equal to 10. The left-hand term of our interval is 8 since it is the lower bound for our set, and there is a bracket around it since it is in our set (8 is greater than or equal to 8). The right-hand term of our interval is 10 since it is the upper bound for our set, and there is also a bracket around it since it is in our set (10 is less than or equal to 10).
Example Question #6 : Linear Inequalities
Express the following linear inequality in interval notation.
Upon solving for x, we find that 1 is less than x which is less than or equal to 5, or x is greater than 1 AND x is less than or equal to 5. The left-hand term of our interval is 1 since it is the lower bound for our set, and there is a parenthesis around it since it is not in our set (1 is not greater than 1). The right-hand term of our interval is 5 since it is the upper bound for our set, and there is a bracket around it since it is in our set (5 is less than or equal to 5). Remember when dividing or multiplying an inequality by a negative number to switch the direction of the inequalities.
Example Question #7 : Linear Inequalities
Express the following linear inequality in interval notation.
Upon solving for x, we find that -1 is less than or equal to x which is less than 2, or x is greater than or equal to -1 AND x is less than 2. The left-hand term of our interval is -1 since it is the lower bound for our set, and there is a bracket around it since it is in our set (-1 is greater than or equal to -1). The right-hand term of our interval is 2 since it is the upper bound for our set, and there is a parenthesis around it since it is not in our set (2 is not less than 2). Remember when dividing or multiplying an inequality by a negative number to switch the direction of the inequalities.
Example Question #8 : Linear Inequalities
Express the following linear inequality in interval notation.
 or
or 
Upon solving for x, we find that x is less than or equal to -2 OR x is greater than 1. Since x may be in either of those sets, we must take the union of the sets. The first interval begins with negative infinity, since x can be anything less than -2. The first interval ends at -2 and includes it in the set, so there is a bracket around it. We join this interval with the second interval beginning with 1, and there is a parenthesis around 1 since it is not in the set. The second interval ends with infinity since any number larger than 1 is in our set. There are always parenthesis around infinities.
Example Question #9 : Linear Inequalities
Express the following linear inequality in interval notation.
 or
or 
Upon solving for x, we find that x is less than or equal to -7/2 OR x is greater than or equal to 1/2. Since x may be in either of those sets, we must take the union of the sets. The first interval begins with negative infinity, since x can be anything less than -7/2. The first interval ends at -7/2 and includes it in the set, so there is a bracket around it. We join this interval with the second interval beginning with 1/2, and there is a bracket around 1/2 since it is in the set. The second interval ends with infinity since any number larger than 1/2 is in our set. There are always parenthesis around infinities.
Certified Tutor
Certified Tutor
All College Algebra Resources

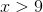
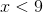
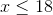











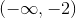

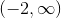

![\left [ -2,\infty \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009903/gif.latex)

![(-\infty ,-5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009929/gif.latex)

![(-\infty ,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009926/gif.latex)





![(-\infty ,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010067/gif.latex)



![[8,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010205/gif.latex)

![[2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010207/gif.latex)

![(8,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010209/gif.latex)



![(1,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010345/gif.latex)

![[1,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010346/gif.latex)

![(3,6]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010354/gif.latex)

![(-2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010353/gif.latex)
![(-1,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010351/gif.latex)


![(-\infty ,-2]\cup (1,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010355/gif.latex)
![(-\infty ,-1]\cup (2,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010357/gif.latex)
![(-\infty ,-3]\cup (6,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010359/gif.latex)

![(-\infty ,-\frac{3}{2}]\cup[\frac{5}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010363/gif.latex)
![(-\infty ,-\frac{5}{2}]\cup[\frac{3}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010362/gif.latex)
![(-\infty ,-\frac{7}{2}]\cup[\frac{1}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010360/gif.latex)
![(-\infty ,-\frac{1}{2}]\cup[\frac{7}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010361/gif.latex)
![(-\infty ,-6]\cup[2,\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010364/gif.latex)



