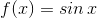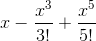We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Taylor and Maclaurin Series

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Maclaurin Series

Write out the first two terms of the Maclaurin series of the following function:

f(x)=x^3+2x^2+1

Possible Answers:

0-1

1+0

0+0

0+1

Correct answer:

1+0

Explanation:

The Maclaurin series of a function is simply the Taylor series of a function, but about x=0 (so a=0 in the formula):

$\sum_{n=0}^{\infty }\frac{f^{n}(a)(x-a)^{n}}{n!}$

To write out the first two terms (n=0 and n=1), we must find the first derivative of the function (because the zeroth derivative is the function itself):

f'(x)=3x^2+4x

The derivative was found using the following rule:

$\frac{d}{dx}(x^n)=nx^{n-1}$

Next, use the general form, plugging in n=0 for the first term and n=1 for the second term:

$\frac{(0 + 0+1)(x)^0}{0!}+\frac{(0+0)(x^1)}{1!}=1+0$

Report an Error

Example Question #3091 : Calculus Ii

Find the Maclaurin series for the function:

$\frac{1}{e^x}$

Possible Answers:

$\sum_{n=0}^{\infty}(-1)^n\frac{x^n}{(2n)!}$

$\sum_{n=0}^{\infty}\frac{x^n}{n!}\:ln(n)$

$\sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!\:ln(n)}$

$\sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!}$

$\sum_{n=0}^{\infty}(-1)^nx^n$

Correct answer:

$\sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!}$

Explanation:

Write Maclaurin series generated by a function f. The Maclaurin series is centered at a=0 for the Taylor series.

$\sum_{b=0}^{\infty}\frac{f^b(a=0)}{b!}x^b=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...$

Evaluate the function and the derivatives of $f(x)=\frac{1}{e^x}$ at x=0 .

$f(x=0)=e^{-x}=e^0=1$

$f'(x=0)= -e^{-x}= -\frac{1}{e^0}= -1$

$f''(x=0)=e^{-x}=e^0=1$

Substitute the values into the power series. The series pattern can be seen as alternating and increasing order.

$1-x+\frac{x^2}{2!}-\frac{x^3}{3!}+\frac{x^4}{4!}... =\sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!}$

Report an Error

Example Question #10 : Maclaurin Series

Find the first three terms of the Maclaurin series for the following function:

$f(x)=\cos(x)+x^2$

Possible Answers:

$1+0+\frac{x^2}{4}$

$0+0+\frac{1}{2}$

0+0+0

1+0

Correct answer:

$1+0+\frac{x^2}{4}$

Explanation:

The Maclaurin series of a function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

First, we can find the zeroth, first, and second derivatives of the function (n=0, 1, and 2 are the first three terms).

f^0=cos(0)+0^2=1

f^1=-sin(0)+2(0)=0

f^2=-cos(0)+2=1

Plugging these values into the formula we get the following.

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

$f^0(0)+f^1(0)\frac{(x-0)^1}{1!}+f^2(0)\frac{(x-0)^2}{2!}$

$1+0+\frac{x^2}{4}$

Report an Error

Example Question #301 : Series In Calculus

Write out the first three terms of the Maclaurin series of the following function:

$f(x)=\sin(x)$

Possible Answers:

0+x+0

0-x+0

0-1+0

0+0+0

Correct answer:

0+x+0

Explanation:

The Maclaurin series of a function is simply the Taylor series of a function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

Because we were asked to find the first three terms (n=0 to n=2), we must find the zeroth, first, and second derivatives of the function. The zeroth derivative is just the function itself.

$f'(x)=\cos(x)$

$f''(x)=-\sin(x)$

Now plug in x=a=0 into the formula and write out the first three terms (n=0, 1, 2):

$\frac{0(x)^0}{0!}+\frac{1(x)^1}{1!}+\frac{0(x)^2}{2!}=0+x+0$

Report an Error

Example Question #11 : Maclaurin Series

Write out the first three terms for the Maclaurin series of the following function:

$f(x)=10\cos(x)$

Possible Answers:

0+10x+0

10+0-5x^2

0+0+0

10+0+5x^2

Correct answer:

10+0-5x^2

Explanation:

The Maclaurin series for any function is simply the Taylor series of the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We first must find the zeroth, first, and second derivative of the function (for n=0, 1, and 2). The zeroth derivative is the function itself:

$f'(x)=-10\sin(x)$

$f''(x)=-10\cos(x)$

The derivatives were found using the following rules:

$\frac{\mathrm{d}}{\mathrm{d} x}\sin(x)=\cos(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x}\cos(x)=-\sin(x)$

Now, we just use the formula, with x=a=0 , to write out the first three terms of the series (n=0, 1, and 2):

$\frac{10(1)(x)^0}{0!}-\frac{10(0)(x)^1}{1!}-\frac{10(1)(x)^2}{2!}=10+0+5x^2$

Report an Error

Example Question #312 : Series In Calculus

Write the first two terms Maclaurin series of the following function:

$f(x)=x\cos(x)$

Possible Answers:

0+0

0-x

x+1

0+x

Correct answer:

0+x

Explanation:

The Maclaurin series for a function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We must find the first two terms of the series, corresponding to n=0 and n=1. We need the zeroth and first derivative of the function, the zeroth derivative being the the function itself:

$f'(x)=\cos(x)-x\sin(x)$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$

Now, use the formula above to write out the first two terms:

$\frac{0(x)^0}{0!}+\frac{1(x)^1}{1!}=0+x$

Report an Error

Example Question #311 : Series In Calculus

Write out the first five terms of the Maclaurin series for the following function:

$f(x)=\cos(x)$

Possible Answers:

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

$1+0+\frac{x^2}{2}+0+\frac{x^4}{4}$

$0+x+0+\frac{x^3}{6}+0$

0+0+0+0+0

Correct answer:

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

Explanation:

The Maclaurin series for any function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

First, we must find the zeroth through fourth derivative of the function. The zeroth derivative is simply the function itself.

$f'(x)=-\sin(x)$

$f''(x)=-\cos(x)$

$f'''(x)=\sin(x)$

$f^4(x)=\cos(x)$

The following rules were used for the derivatives:

$\frac{d}{dx}\cos(x)=-\sin(x)$ , $\frac{d}{dx}\sin(x)=-\cos(x)$

Next, we simply evaluate all of the derivatives at x=a=0 and then write out all of the terms:

$\frac{1(x)^0}{0!}-\frac{0(x)^1}{1!}-\frac{1(x)^2}{2!}+\frac{0(x)^3}{3!}+\frac{1(x)^4}{4!}$

which simplified is equal to

$1+0-\frac{x^2}{2}+0+\frac{x^4}{24}$

Report an Error

Example Question #314 : Series In Calculus

Write out the first four terms of the Maclaurin series for the following function:

f(x)=2x^2+x+1

Possible Answers:

0+x+2x^2+0

1+x+2x^2+0

0+0+0+0

1+x+4x^2+0

Correct answer:

1+x+2x^2+0

Explanation:

The Maclaurin series is the Taylor series for a function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

We need to find the zeroth, first, second, and third derivative of the function (n=0, 1, 2, and 3). The zeroth derivative is simply the function itself.

f'(x)=4x+1

f''(x)=4

f'''(x)=0

The derivatives were found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Now, use the above formula, with x=a=0 to write out the first four terms:

$\frac{(1)(x)^0}{0!}+\frac{1(x)^1}{1!}+\frac{4(x)^2}{2!}+\frac{0(x)^3}{3!}$

which simplified becomes

1+x+2x^2+0

Report an Error

Example Question #315 : Series In Calculus

Write the first two terms of the Maclaurin series for the following function:

$f(x)=2x^2-\cos(x)$

Possible Answers:

1+0

-1+0

0+1

0+0

Correct answer:

-1+0

Explanation:

The Maclaurin series for any function is simply the Taylor series for the function about a=0:

$\sum_{n=0}^{\infty }f^{(n)}(a)\frac{(x-a)^n}{n!}$

For the first two terms (n=0, 1) we must find the zeroth and first derivative of the function. The zeroth derivative is just the function itself.

$f'(x)=4x+\sin(x)$

Now, using the above formula, write out the first two terms:

$\frac{-1(x)^0}{0!}+\frac{0(x)^1}{1!}=-1+0$

Report an Error

Example Question #52 : Taylor Series

Find the Maclaurin Series of the function

$f(x)=sin\,x$

up to the fifth degree.

Possible Answers:

DNE

$1-\frac{x^2}{2!}+\frac{x^4}{4!}$

$x+\frac{x^2}{2!}-\frac{x^3}{3!}-\frac{x^4}{4!}+\frac{x^5}{5!}$

$x-\frac{x^3}{3!}+\frac{x^5}{5!}$

Correct answer:

$x-\frac{x^3}{3!}+\frac{x^5}{5!}$

Explanation:

The formula for an i-th degree Maclaurin Polynomial is

$f(x)=\sum_{n=0}^{i}\frac{f^{(n)}(0)}{n!}x^n$

For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.

$\begin{matrix} f(0)=sin(0)=0\\ f'(0)=cos(0)=1\\ f''(0)=-sin(0)=0\\ f'''(0)=-cos(0)=-1\\ f^{(4)}=sin(0)=0 \\ \end{matrix}$

$f^{(5)}(0)=cos(0)=1$

The summation becomes

$\sum_{n=0}^{5}\frac{f^{(n)}(0)}{n!}x^n=\frac{f(0)}{0!}x^0+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5$

And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial

$f(x)=sin(x)\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}$

Report an Error

View Calculus 2 Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

View Calculus 2 Tutors

Jason
Certified Tutor

Brigham Young University, Bachelor, Neuroscience.

View Calculus 2 Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Denver, Spanish Tutors in Denver, French Tutors in New York City, Computer Science Tutors in San Francisco-Bay Area, ISEE Tutors in San Francisco-Bay Area, Biology Tutors in Atlanta, Biology Tutors in Boston, SSAT Tutors in San Diego, GRE Tutors in Denver, Calculus Tutors in Chicago

Popular Courses & Classes

GMAT Courses & Classes in Denver, Spanish Courses & Classes in Denver, SAT Courses & Classes in Seattle, ACT Courses & Classes in San Diego, SAT Courses & Classes in Boston, Spanish Courses & Classes in Seattle, ISEE Courses & Classes in New York City, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in Denver, SAT Courses & Classes in Chicago

Popular Test Prep

SAT Test Prep in Boston, GRE Test Prep in Atlanta, SAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Miami, GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Atlanta, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Atlanta, ISEE Test Prep in Houston, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Taylor and Maclaurin Series

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #1 : Maclaurin Series

Example Question #3091 : Calculus Ii

Example Question #10 : Maclaurin Series

Example Question #301 : Series In Calculus

Example Question #11 : Maclaurin Series

Example Question #312 : Series In Calculus

Example Question #311 : Series In Calculus

Example Question #314 : Series In Calculus

Example Question #315 : Series In Calculus

Example Question #52 : Taylor Series

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: