All Calculus 2 Resources
Example Questions
Example Question #46 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function. Write the integral expression:
Now integrate:
Plug in your initial conditions to find C:
Plug your C into the position function:
Example Question #221 : Integrals
If 

Recall that the integral of velocity is position. Therefore, write the integral expression:
Integrate. Remember to raise the exponent by 1 and also put that result on the denominator:
Now, plug in your initial conditions:
Plug your C back in to your position function:
Example Question #48 : Applications In Physics
If 

Recall that the integral of velocity is position. Therefore, write your integral expression:
Now, integrate:
Plug in your initial conditions to find C:
Plug your C back into your position function:
Example Question #49 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function. Therefore, write your integral expression:
Integrate:
Plug in your initial conditions to find C:
Plug C back in to your position function:
Example Question #50 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function:
Now, integrate:
Plug in your initial conditions to get your C:
Plug your C back into the position function:
Example Question #51 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function:
Now, integrate:
Now plug in your initial conditions:
Plug your C back into your position function:
Example Question #52 : Applications In Physics
If 

Recall that the integral of velocity is the position function:
Now, integrate. Remember to raise the exponent by 1 and also put that result on the denominator:
Now plug in your initial conditions to solve for C:
Now plug your C back in to your position function:
Example Question #53 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function:
Now, integrate. Remember to raise the exponent by 1 and also put that result on the denominator:
Now, plug in your initial conditions:
Now plug your C back into your position function:
Example Question #54 : Applications In Physics
In the vacuum of space, a particle is initially moving at a constant speed of only 6 meters/second away from you as you watch in your space capsule stationary relative to the particle. You track the object and then observe an acceleration that varies with time as,
After travelling for 20 minutes at this speed the particle is now 
To solve the problem we first need to find the position function by successively integrating. First find the velocity function by integrating the acceleration:
The constant of integration 
Now we integrate the velocity function to find the position function:
The constant of integration 







Now solve for
Example Question #51 : Integral Applications
Give the area of the region bounded by the curves of the functions
and

The two curves intersect when 
Therefore, the area between the curves is
All Calculus 2 Resources































































































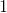





![\left |\int_{1}^{3} \left [g(x) - f(x) \right ] \mathrm{d}x \right |](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/180811/gif.latex)









