All Basic Geometry Resources
Example Questions
Example Question #3 : How To Find If Right Triangles Are Similar
Two triangles, 

Their corresponding angles are equal AND their corresponding lengths are proportional.
Their corresponding angles are equal.
Their corresponding angles are equal AND their corresponding lengths are equal.
Their corresponding lengths are proportional.
Their corresponding angles are equal AND their corresponding lengths are proportional.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. Either condition alone is not sufficient. If two figures have both equal corresponding angles and equal corresponding lengths then they are congruent, not similar.
Example Question #1181 : Plane Geometry



Are 

Yes, because 

There is not enough information given to answer this question.
No, because 

Yes, because 

There is not enough information given to answer this question.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. In other words, we need to know both the measures of the corresponding angles and the lengths of the corresponding sides. In this case, we know only the measures of 

It's not enough to know that both figures are right triangles, nor can we assume that angles are the same measurement because they appear to be.
Similar triangles do not have to be the same size.
Example Question #1182 : Plane Geometry



What is the length of 
Since 












Substitute the known values.
Cross-multiply and simplify.





Example Question #1 : How To Find If Right Triangles Are Similar
Are these triangles similar? Give a justification.
No - the angles are not the same
Yes - they LOOK like they're similar
Not enough information - we would need to know at least one side length in each triangle
Yes - the triangles are similar by AA
No - the side lengths are not proportional
Yes - the triangles are similar by AA
These triangles were purposely drawn misleadingly. Just from glancing at them, the angles that appear to correspond are given different angle measures, so they don't "look" similar. However, if we subtract, we figure out that the missing angle in the triangle with the 66-degree angle must be 24 degrees, since 
Example Question #1181 : Basic Geometry
Are these triangles similar? If so, list the scale factor.
Yes-scale factor
Yes - scale factor
No
Yes - scale factor
Cannot be determined - we need to know all three sides of both triangles
Yes - scale factor
The two triangles are similar, but we can't be sure of that until we can compare all three corresponding pairs of sides and make sure the ratios are the same. In order to do that, we first have to solve for the missing sides using the Pythagorean Theorem.
The smaller triangle is missing not the hypotenuse, c, but one of the legs, so we'll use the formula slightly differently.

Now we can compare all three ratios of corresponding sides:

We can simplify the leftmost ratio by dividing top and bottom by 3 and getting 
We can simplify the middle ratio by dividing top and bottom by 4 and getting 
Finally, we can simplify the ratio on the right by dividing top and bottom by 5 and getting 
This means that the triangles are definitely similar, and 
Example Question #2 : How To Find If Right Triangles Are Similar
Are these right triangles similar? If so, state the scale factor.
No - the side lengths are not proportional
Yes - scale factor
Yes - scale factor
Yes - scale factor
Not enough information to be determined
No - the side lengths are not proportional
In order to compare these triangles and determine if they are similar, we need to know all three side lengths in both triangles. To get the missing ones, we can use Pythagorean Theorem:

The other triangle is missing one of the legs rather than the hypotenuse, so we'll adjust accordingly:

Now we can compare ratios of corresponding sides:
The first ratio simplifies to 
Example Question #5 : Right Triangles
Given: 



True or false: From the given information, it follows that 
False
True
True
If we seek to prove that 






By the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion with the corresponding sides of another triangle, and the included angles are congruent, then the triangles are similar.






Example Question #11 : Right Triangles

Refer to the above diagram.
True or false:
True
False
True
The distance from the origin to 
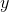


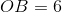




According to the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion to the corresponding sides of a second triangle, and their included angles are congruent, the triangles are similar.
We can test the proportion statement
by substituting:
Test the truth of this statement by comparing their cross products:
The cross-products are equal, making the proportion statement true, so two pairs of sides are in proportion. Also, their included angles 


Example Question #201 : Triangles

Refer to the above figure.
True, false, or inconclusive: 
False
Inconclusive
True
True



Example Question #1182 : Basic Geometry
What is the length of the remaining side of the right triangle?
Rearrange the Pythagorean Theorem to find the missing side. The Pythagorean Theorem is:
where 


Certified Tutor
All Basic Geometry Resources
























































