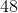We first multiply the numerators:

Then we multiply the denominators:

The resulting fraction is:

We divide the numerator and denominator by 12.

The numerator is:

The denominator results in:

Our resulting fraction is:

First, multiply the numerators of each term:

Then, multiply the denominators:

This results in a fraction of . Since the numerator and denominator both have a common factor of 4, reduce both the numerator and denominator by dividing by 4 to get the simplest form fraction .

First, multiply the terms in the numerators:

Then multiply the terms in the denominators:

This results in the fraction  .

Notice that both the numerator and denominator have a common factor of 6. Dividing both the numerator and denominator by 6 results in the simplest form fraction .

First, multiply the numerators of the terms:

Then, multiply the denominators of the terms:

The resulting fraction is . Note that the numerator and denominator both have a common factor of 6. Dividing both parts of the fraction by 6, we get the simplest form fraction .

To easily express a fraction as a decimal, we need to convert the denominator into a power of . We can do this by dividing both the top and the bottom of the given fraction by  to express it in tenths.

, or six tenths, can be expressed as .

The correct answer is 

is greater than half so you can eliminate  and  right away.

You should memorize common fractions:

The best way to answer this question is to find the smallest fraction among the answer choices.

Comparing fractions can be done easily when they are converted to decimals.

Of these options, only , or 0.60, is less than .

The correct answer is 36. The best way to approach this problem is to take each denominator and list out its multiples. You can then find the common multiple between each denominator. 

Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48

Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42

Multiples of 12: 12, 24, 36, 48, 60

Multiples of 36: 36, 72, 108

Multiples of 18: 18, 36, 54, 72

From the above multiples, we can see that the least common denominator is 36.

The least common denominator is the lowest number that has each denominator is a potential factor.

1. Multiply the two lowest denominators:

2. Check to see if the other denominators can factor into that denominator:

So 24 is your least common denominator. (48 is also a common denominator of all of these fractions, but it is not the lowest one)

To find the least common denominator, list out the multiples of both denominators until you find the smallest multiple that is shared by both.

4: 4, 8, 12, 16, 20, 24, 28, 32

7: 7, 14, 21, 28, 35

Because 28 is the first shared multiple of 4 and 7, it must be the least common denominator for these two fractions.