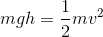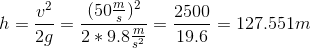Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C: Mechanics : AP Physics C

Study concepts, example questions & explanations for AP Physics C: Mechanics

Create An Account

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Friction

$\begin{align*}&\text{A block of mass }19kg\text{ rests on an incline of }69^{\circ}\\&\text{What is the frictional force acting on the block from the surface?}\\&g=9.81\frac{m}{s^2}\end{align*}$

Possible Answers:

186.39N

174.01N

66.8N

6.81N

Correct answer:

174.01N

Explanation:

Normal

Report an Error

Example Question #91 : Mechanics Exam

$\begin{align*}&\text{A block of mass }284kg\text{ rests on an incline of }48^{\circ}\\&\text{It is also partially supported by a rope.}\\&\text{The frictional force acting on the block is }207.04N\\&\text{What is the tension felt in the rope?}\\&g=9.81\frac{m}{s^2}\end{align*}$

Possible Answers:

2507.44N

2070.43N

1864.22N

2786.04N

Correct answer:

2507.44N

Explanation:

Normalwrope

$\begin{align*}&\text{To solve a problem of force balance, a good idea is to draw}\\&\text{it out. Since the block is at rest, i.e. stationary, the sum}\\&\text{of forces acting on it must be equal to zero. The forces acting}\\&\text{on it are gravity (in the form of the mass times the gravitational}\\&\text{constant), the force of the rope supporting it, a normal force,}\\&\text{and since it’s on an incline, a frictional force to balance}\\&\text{it all out. Notice that the tension in the rope mitigates some}\\&\text{of the gravitational force (as illustrated in the upper left}\\&\text{corner) to lessen what is applied to the slope:}\\&F_{mass}=m*g\\&F_{normal}=(F_{mass}-F_{rope})*cos(a)\\&F_{friction}=(F_{mass}-F_{rope})*sin(a)\\&F_{rope}=F_{mass}-\frac{F_{friction}}{sin(a)}\\&F_{rope}=2786.04N-\frac{207.04N}{sin(48^{\circ})}\\&F_{rope}=2507.44N\end{align*}$

Report an Error

Example Question #4 : Friction

$\begin{align*}&\text{A block of mass }101kg\text{ rests on an incline of }68^{\circ}\\&\text{It is also partially supported by a rope with a tension of }693.57N\\&\text{What is the frictional force acting on the block from the surface?}\\&g=9.81\frac{m}{s^2}\end{align*}$

Possible Answers:

918.66N

111.35N

275.6N

371.16N

Correct answer:

275.6N

Explanation:

Normalwrope

$\begin{align*}&\text{To solve a problem of force balance, a good idea is to draw}\\&\text{it out. Since the block is at rest, i.e. stationary, the sum}\\&\text{of forces acting on it must be equal to zero. The forces acting}\\&\text{on it are gravity (in the form of the mass times the gravitational}\\&\text{constant), the force of the rope supporting it, a normal force,}\\&\text{and since it’s on an incline, a frictional force to balance}\\&\text{it all out. Notice that the tension in the rope mitigates some}\\&\text{of the gravitational force (as illustrated in the upper left}\\&\text{corner) to lessen what is applied to the slope:}\\&F_{mass}=m*g\\&F_{normal}=(F_{mass}-F_{rope})*cos(a)\\&F_{friction}=(F_{mass}-F_{rope})*sin(a)\\&F_{friction}=(101kg(9.81\frac{m}{s^2})-693.57N)(sin(68^{\circ}))\\&F_{friction}=275.6N\end{align*}$

Report an Error

Example Question #11 : Forces

$\begin{align*}&\text{A block of mass }187kg\text{ rests on an incline of }70^{\circ}\\&\text{What is the frictional force acting on the block from the surface?}\\&g=9.81\frac{m}{s^2}\end{align*}$

Possible Answers:

63.96N

627.43N

1723.84N

1834.47N

Correct answer:

1723.84N

Explanation:

Normal

Report an Error

Example Question #93 : Mechanics Exam

$\begin{align*}&\text{A block of mass }208kg\text{ rests on an incline of }28^{\circ}\\&\text{What is the frictional force acting on the block from the surface?}\\&g=9.81\frac{m}{s^2}\end{align*}$

Possible Answers:

2040.48N

957.95N

1801.64N

183.65N

Correct answer:

957.95N

Explanation:

Normal

Report an Error

Example Question #91 : Ap Physics C

A block with a mass of 10kg is traveling at $50\frac{m}{s}$ when it impacts the ground. From how many meters off the ground was the block dropped?

Round to the nearest whole number.

Possible Answers:

130m

132m

126m

124m

128m

Correct answer:

128m

Explanation:

Set the gravitational potential energy and kinetic energy equal to each other and solve for the height.

$mgh = \frac{1}{2}mv^2$

Mass cancels.

$gh = \frac{1}{2}v^2$

Isolate the height and plug in our values.

$h = \frac{v^2}{2g} = \frac{(50\frac{m}{s})^2}{2*9.8\frac{m}{s^2}} = \frac{2500}{19.6} = 127.551m$

Rounding this gives h = 128m .

Report an Error

Example Question #92 : Ap Physics C

An object of mass $\small m$ is dropped from a tower. The object's drag force is given by $\small F_{d}=-bv^{2}$ where $\small b$ is a positive constant. What will the objects terminal velocity be?

Possible Answers:

$v_{term}=\sqrt{\frac{mg}{b}}$

$\small v_{term}=\sqrt{\frac{g}{b}}$

$\small \small v_{term}=\frac{mg}{b}$

$\small \small v_{term}=\frac{g}{b}$

$\small \small v_{term}=\sqrt{\frac{b}{mg}}$

Correct answer:

$v_{term}=\sqrt{\frac{mg}{b}}$

Explanation:

To find terminal velocity, set the magnitude of the drag force equal to the magnitude of the force of gravity since when these forces are equal and opposite, the object will stop accelerating:

$\small F_{d}=mg$

$\small bv^{2}=mg$

Solve for

$v=\sqrt{\frac{mg}{b}}$

Report an Error

Example Question #1 : Gravity

A ship of mass $\small m$ and an initial velocity of $\small v_0$ is coasting to a stop. The water exerts a drag force on the ship. The drag force is proportional to the velocity:

F_D =-kv where the negative sign indicates that the drag force acts in a direction opposite the motion. After the ship has coasted for a time equal to $\frac{2}{k}$ , how fast (in terms of $\small v_0$ ) will the ship be moving?

Possible Answers:

$\small \frac{v_0}{4}$

$\small 0.135 v_0$

$\small 0.63v_0$

$\small 0.37v_0$

$\small \frac{v_{0}}2{}$

Correct answer:

$\small 0.135 v_0$

Explanation:

The ship's equation of velocity (found by solving the first-order differential equation) is $\small v=v_0e^{-kt}$

Substitute $t=\frac{2}{k}$ and solve.

Report an Error

Example Question #93 : Ap Physics C

A spherical asteroid has a hole drilled through the center as diagrammed below:

Hole through planet

Refer to the diagram above. An object that is much smaller than the asteroid is released from rest at the surface of the asteroid, at point a. How do the velocity and acceleration of the object compare at point b at the surface, and point a, located at the center of the asteroid?

Possible Answers:

$v_{a}<v_{b}$ and $a_{a}=a_{b}$

$v_{a}<v_{b}$ and $a_{a}>_{b}$

$v_{a}=v_{b}$ and $a_{a}=a_{b}$

$v_{a}< v_{b}$ and $a_{a}< a_{b}$

$v_{a}=v_{b}$ and $a_{a}< a_{b}$

Correct answer:

$v_{a}<v_{b}$ and $a_{a}>_{b}$

Explanation:

Because the gravitational force depends only on the mass beneath the object (which is the gravitational version of Gauss's Law for charge), the acceleration steadily decreases as the object falls, and drops to zero at the center. Nevertheless, the velocity keeps increasing as the object falls, it just does so more slowly.

Report an Error

Example Question #1 : Gravity

With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?

The mass of the moon is $7.2*10^{22}kg$ and its radius is 1.8*10^6m .

$\small G=6.67*10^{-11}\frac{m^2N}{kg^2}$

Possible Answers:

$1.6\frac{km}{s}$

$520\frac{m}{s}$

$470\frac{m}{s}$

$730\frac{m}{s}$

$2.3\frac{km}{s}$

Correct answer:

$2.3\frac{km}{s}$

Explanation:

Relevant equations:

$E_{total}=K+U_g$

$K = \frac{1}{2}mv^2$

$U_g=\frac{-GMm}{r}$

For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.

For the minimum energy case as the rocket leaves the surface:

$0 = K + U_g = \frac{1}{2}mv_{esc}^2 - \frac{GMm}{r}$

Rearrange energy equation to isolate the velocity term.

$v_{esc}^2 = \frac{GMm}{\frac{1}{2}mr}$

$v_{esc}=\sqrt{\frac{2GM}{r}}$

Substitute in the given values to solve for the velocity.

$v_{esc}=\sqrt{\frac{2(6.67*10^{-11}\frac{m^2N}{kg^2})(7.2*10^{22}kg)}{(1.8*10^6m)}}=2310\frac{m}{s}\approx 2.3\frac{km}{s}$

Report an Error

View Tutors

Ekomobong
Certified Tutor

Howard University, Bachelor of Engineering, Electrical Engineering.

View Tutors

Millat
Certified Tutor

Rensselaer Polytechnic Institute, Bachelor in Arts, Biomedical Engineering.

View Tutors

Samantha
Certified Tutor

Middle Tennessee State University, Bachelor in Arts, History.

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in New York City, LSAT Tutors in Denver, GRE Tutors in Boston, Reading Tutors in San Francisco-Bay Area, Chemistry Tutors in Miami, SAT Tutors in Chicago, Statistics Tutors in San Francisco-Bay Area, Math Tutors in San Francisco-Bay Area, GRE Tutors in New York City, French Tutors in Dallas Fort Worth

Popular Courses & Classes

GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Denver, ISEE Courses & Classes in Denver, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Washington DC, ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Houston, ISEE Test Prep in Denver, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Chicago, MCAT Test Prep in Miami, GRE Test Prep in Los Angeles, ISEE Test Prep in Boston, ACT Test Prep in Boston, SSAT Test Prep in Denver, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C: Mechanics : AP Physics C

Study concepts, example questions & explanations for AP Physics C: Mechanics

All AP Physics C: Mechanics Resources

Example Questions

Example Question #2 : Friction

Example Question #91 : Mechanics Exam

Example Question #4 : Friction

Example Question #11 : Forces

Example Question #93 : Mechanics Exam

Example Question #91 : Ap Physics C

Example Question #92 : Ap Physics C

Example Question #1 : Gravity

Example Question #93 : Ap Physics C

Example Question #1 : Gravity

All AP Physics C: Mechanics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: