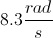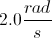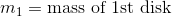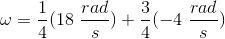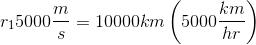All AP Physics C Electricity Resources
Example Questions
Example Question #21 : Rotational Motion And Torque
An ice skater begins to spin, starting with his arms spread out as far as possible, parallel to the ice. He pulls his arms into his body, and then raises them completely vertically towards the ceiling. As the skater pulls his arms inward, his angular velocity will __________, and as he raises his arms vertically his angular velocity will __________.
decrease . . . increase
increase . . . decrease
increase . . . stay the same
decrease . . . stay the same
increase . . . stay the same
Through conservation of angular momentum, as moment of inertia decreases, the angular velocity increases. Moment of inertia is dependent on the distribution of the spinning body's mass away from the center of mass—as the skater brings his arms in, he lowers his moment of inertia, thus increasing his angular velocity. If he raises his arms completely vertically from this point, it does not change the radius of mass distributions (from the center of his body), thus maintaining his angular velocity.
Example Question #2 : Understanding Conservation Of Angular Momentum
Sarah spins a ball of mass 




By the conservation of angular momentum, the angular momentum 
Here, 


Substitute.
We are given that 

Example Question #72 : Motion

A child is standing at the center of a frictionless, rotating platform. Both the child and the platform are rotating with and initial angular velocity, 
Total momentum
Total angular inertia
Total rotational kinetic energy
Total angular momentum
Rotational inertia of the disk
Total rotational kinetic energy
Since the platform is frictionless, as the child walks, angular momentum is conserved. However, since there is an 

Example Question #1 : Using Angular Momentum Equations
Two solid cylinderical disks have equal radii. The first disk is spinning clockwise at 

For the first disk, we have the information below.
For the second disk, we have the information below.
(The minus sign indicates counterclockwise while the positive indicates clockwise.)
To do this problem, we use conservation of angular momentum. Before the disks are put in contact, the initial total angular momentum is given by the equation below.
It is just the sum of the angular momentums of each disk. When the disks are combined together, then final angular momentum can be found by the following equation.
Set this equal to the initial angular momentum.
Simplify and solve for 
Example Question #22 : Rotational Motion And Torque
A piece of space debris is travelling in an elliptical orbit around a planet. At its closest point to the planet, the debris is travelling at 


The equation for conservation of angular momentum is:
This means that the angular momentum of the object at the two points in its orbit must be the same. Since the mass of the debris does not change, this gives us an equality of the product of the velocity and distance of the debris at any two points of its orbit:

Plug in known values.
There is disagreement between units; the velocities are given in both 

Solve for 
Example Question #1 : Interpreting Rotational Motion And Torque Diagrams
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
Using a longer wrench
Pulling or pushing at an angle that is more perpendicular to the wrench
Pulling or pushing at an angle that is less perpendicular to the wrench
Using a wrench of a different material
Increasing the magnitude of the force he puts on the wrench
Pulling or pushing at an angle that is less perpendicular to the wrench
Remember the torque equation:
Exerting force on the wrench at an angle less perpendicular to the wrench will reduce 
The other answer options will all increase the torque being applied, making the twisting motion easier.
Example Question #71 : Ap Physics C
Weightlessness is experienced when the normal force equals __________.
zero
the mass of the object
a negative value
the force due to gravity
zero
"Weightlessness" is analogous to free-fall (neglecting air resistance), during which the only force on an object is the force of gravity. When normal force becomes zero, the object loses physical contact with the surface.
When normal force is equal to the force of gravity, the object is in equilibrium and the net vertical force is zero. This results in zero acceleration, but does not result in "weightlessness." Mass is not a force, and negative force values merely indicate relative direction (assuming correct calculations)
Example Question #2 : Forces
A book of mass 1kg is held to a vertical wall by a person's hand applying a 20N force directly toward the wall. The wall has a static friction coefficient of 0.3 and a kinetic friction coefficient of 0.2. With the book held at rest, what the is frictional force keeping the book from sliding down the wall?
Frictional force is calculated using the normal force and the friction coefficient. Since the book is at rest (not in motion), we use the coefficient of static friction.
The normal force will be equal and opposite the force pushing directly into the surface; in this case, that means the normal force will be 20N.
Solve for the force of friction:
Example Question #3 : Forces

Example Question #1 : Friction And Normal Force

All AP Physics C Electricity Resources