All AP Physics 2 Resources
Example Questions
Example Question #442 : Ap Physics 2
A ray of light is traveling through air at an angle of 
This problem can be solved using Snell's law:
Rearrange to solve for for the index of refraction of water
We can determine the second angle:
We have all the values for Snell's law, allowing us to solve:
Example Question #443 : Ap Physics 2
A beam of light going through a medium with an index of refraction of 1.14 has an angle of incidence of 

There is not enough information to determine the index of refraction.
To find the index of refraction, we use Snell's Law:
We have values for 



Now, we can just plug in our numbers.
Therefore, the index of refraction of the second material is 1.346.
Example Question #1 : Snell's Law
Find the angle of refraction if a light beam enters water at an angle of 


To find the angle of refraction, use the Snell's law equation to determine the angle.
Find the index of refraction for water.
Find the index of refraction for air.
Solve for 
Example Question #451 : Ap Physics 2
A cup of water sitting on a table outside in the sunlight is filled to the top. The sun happens to be 


This problem is a Snell's Law problem. There is some information not stated but can be found in your text book such as the index of refraction of water. A picture will help us see what is going on in this problem,




First, let's find 
Now apply Snell's Law to find 
Now there is a right triangle with sides 


Example Question #1 : Snell's Law
A ray of light initially travelling through the air enters a material at a angle of 


By Snell's law, we have the relation between the incident angle 



The index of refraction of air is taken to be 
Example Question #1 : Snell's Law
A laser initially moving through air enters a medium that has an index of refraction 

Using Snell's Law, we can use the information given to solve for 
Solve for the incident angle.
Plug in and solve:
Example Question #2 : Snell's Law
Suppose that a ray of light traveling through air strikes the surface of a body of water, and the ray of light then begins traveling through the water. If the ray of light from air hits the surface of the water at an angle of 
This question is presenting us with a scenario in which light is first traveling through air, and then it hits the surface of water and begins traveling through the water. We're provided with the angle of the incident light, and are asked to find the angle of the light with respect to the horizontal after refraction has occurred.
To answer this question, we'll need to make use of Snell's law:
Where 



When establishing the values for the variables listed above, it's important to be aware of the difference between the angle with respect to the horizontal (as presented in the question stem) and the angle with respect to the normal (which is perpendicular to the surface boundary). In the question stem, we're told that the incident light ray strikes the surface boundary at an angle of 

Now, we have all the information we need to solve for the missing angle. But first, we can rearrange the above equation to isolate the variable we're looking for.
But there's one more very important thing we have to do. Recall that the question is asking for the resulting angle with respect to the horizontal, whereas this answer is telling us the angle with respect to the normal. Therefore, we will need to convert this angle:
Example Question #1 : Snell's Law
Light travels from air 


None of these
Snell's Law:
Where




Use Snell's Law
Solve for 
Plug in values:
Solving:
Example Question #9 : Snell's Law
Light travels from air 


None of these
Snell's Law:
Where




Use Snell's Law
Solve for 
Plug in values:
Solve:
Example Question #10 : Snell's Law
Light travels from air 


None of these
Snell's Law:
Where




Use Snell's Law
Solve for 
Plug in values:
All AP Physics 2 Resources






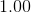






























![\theta_{2}=\arcsin \left [ \frac{n_{1}}{n_{2}}\sin\left ( \theta_{1}\right ) \right ]=27.57^{o}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/549940/gif.latex)





























































