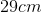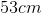All AP Physics 1 Resources
Example Questions
Example Question #1091 : Ap Physics 1
Two masses hang below a massless meter stick. Mass 1 is located at the 10cm mark with a weight of 15kg, while mass 2 is located at the 60cm mark with a weight of 30kg. At what point in between the two masses must the string be attached in order to balance the system?
This problem deals with torque and equilibrium. Noting that the string is between the two masses we can use the torque equation of 


x=43, thus the string is placed at the 43cm mark.
Example Question #91 : Circular And Rotational Motion
An attraction at a science museum helps teach students about the power of torque. There is a long metal beam that has one pivot point. At one end of the bar hangs a full sedan, and on the other end is a rope at which students can pull down, raising the car off the ground.
The beam is 40 meters long and the pivot point is 5 meters from one end. A car of mass 500kg hangs from the short end of the beam. Neglecting the mass of the beam, what is the minimum mass of a student who can hang from the rope and begin to raise the car off the ground?
More information is needed to answer
We are trying to find what force needs to be applied to the rope to result in a net of zero torque on the beam.
Torque applied by the car:
We can use this to find the mass of a student that will create the same amount of torque while hanging from the rope:
Example Question #1 : Torque
There is a 

Bob's mass is
Torque is defined as 

In order for the seesaw to balance, the torque applied by Bob must be equal to 
Example Question #11 : Torque
Terry is pushing a vertical lever that is attached to the floor, and he pushes 


Magnitude of torque can be found by relating the amount of force applied perpendicular to a lever arm about a point of rotation.
In this case, the force is not perpendicular, so we must take the perpendicular aspect of the force to find torque.
Plug in and solve.
Example Question #11 : Torque
From the given force and position vector, calculate the torque experienced by an object.
To calculate the torque experienced by the object, we must take the cross product of the force vector and the position vector.
Example Question #13 : Torque
You apply a force of 

None of these
The definition of torque is
Where


Theta is the angle between the direction of the force and the distance.
In this case, 

Plugging in our remaining values:
Example Question #14 : Torque
There is a steel disk of radius 



Assume
Initial angular momentum is zero
Combine equations:
Solve for
Definition of 
Combine equations:
Plug in values:
Example Question #1092 : Ap Physics 1
A force 




What is the resulting torque in terms of 
The torque 


The new torque, which we will call 



Since 
Example Question #16 : Torque
Find the torque 



Torque is given by:




Example Question #17 : Torque
Consider the following system:

Two spherical masses, A and B, are attached to the end of a rigid rod with length l. The rod is attached to a fixed point, p, which is at a height, h, above the ground. The rod spins around the fixed point in a vertical circle that is traced in grey. 

If the rod is spinning clockwise and has a velocity of 

A system will only have a net torque of 0 when it has no net force or the net force goes through its center of gravity. The only forces applied in this system is from gravity. Therefore, we need to find the orientation at which all gravitational force goes through point p. This occurs when the rod is oriented vertically, thus 
Note: 
Certified Tutor
All AP Physics 1 Resources