All AP Calculus BC Resources
Example Questions
Example Question #1 : Harmonic Series
Determine whether the following series converges or diverges:
The series conditionally converges
The series (absolutely) converges
The series may (absolutely) converge, diverge, or conditionally converge
The series diverges
The series (absolutely) converges
Given just the harmonic series, we would state that the series diverges. However, we are given the alternating harmonic series. To determine whether this series will converge or diverge, we must use the Alternating Series test.
The test states that for a given series 






First, we must evaluate the limit of 
The limit equals zero because the numerator of the fraction equals zero as n approaches infinity.
Next, we must determine if 

Because both parts of the test passed, the series is (absolutely) convergent.
Example Question #1 : Series Of Constants
Determine whether
converges or diverges, and explain why.
More tests are needed.
Convergent, by the alternating series test.
Divergent, by the comparison test.
Divergent, by the test for divergence.
Convergent, by the 
Convergent, by the alternating series test.
We can use the alternating series test to show that
converges.
We must have 


![\small \small \left[0,\frac{\pi}{2}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385614/gif.latex)


![\small \small \left[0,\frac{\pi}{2}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385615/gif.latex)
Now we must show that
1.
2. 
The limit
implies that
so the first condition is satisfied.
We can show that 


The derivative is less than 








converges, by the alternating series test.
Example Question #3 : Alternating Series
For the series: 
The series given is an alternating series.
Write the three rules that are used to satisfy convergence in an alternating series test.
For 
The first and second conditions are satisfied since the terms are positive and are decreasing after each term.
However, the third condition is not valid since 
The correct answer is:
Example Question #1 : Alternating Series With Error Bound
Determine whether the series converges or diverges:
The series is divergent.
The series is conditionally convergent.
The series is (absolutely) convergent.
The series may be convergent, divergent, or conditionally convergent.
The series is divergent.
To determine whether the series converges or diverges, we must use the Alternating Series test, which states that for





For our series,

because it behaves like

The test fails because 
The series is divergent.
Example Question #2 : Abstract Algebra
Which of the following series does not converge?
We can show that the series 
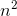

Alternatively, it's clear that 



The other series will converge by alternating series test, ratio test, geometric series, and comparison tests.
Example Question #1 : Concepts Of Convergence And Divergence
One of the following infinite series CONVERGES. Which is it?
None of the others converge.

We start with the equation 





Example Question #2 : P Series
Determine the nature of convergence of the series having the general term:
The series is convergent.
The series is divergent.
The series is convergent.
We will use the Limit Comparison Test to establish this result.
We need to note that the following limit
goes to 1 as n goes to infinity.
Therefore the series have the same nature. They either converge or diverge at the same time.
We will focus on the series:

We know that this series is convergent because it is a p-series. (Remember that

By the Limit Comparison Test, we deduce that the series is convergent, and that is what we needed to show.
Example Question #3 : P Series
Determine if the series converges or diverges. You do not need to find the sum.
Converges
There is not enough information to decide convergence.
Diverges
Neither converges nor diverges.
Conditionally converges.
Converges
We can compare this to the series 
To figure this out, let's first compare 



There is a rule in math that if you take the reciprocal of each term in an inequality, you are allowed to flip the signs.
Thus, 

And so, because 
Example Question #1 : Harmonic Series
Which of the following tests will help determine whether 


P-Series Test: The summation converges since 
Root Test: Since the limit as 
Integral Test: The improper integral determines that the harmonic series diverge.

Integral Test: The improper integral determines that the harmonic series diverge.
The series 
The Nth term test and the Divergent test may not be used to determine whether this series converges, since this is a special case. The root test also does not apply in this scenario.
According the the P-series Test, 


This leaves us with the Integral Test.
Since the improper integral diverges, so does the series.
Example Question #71 : Polynomial Approximations And Series
Does the series 
Cannot tell with the given information.
Converge Absolutely.
Does not exist.
Converge Conditionally.
Diverges.
Converge Conditionally.
The series converges conditionally.
The absolute values of the series 

However, the the limit of the sequence 
Therefore, by the alternating series test, the series converges conditionally.
Certified Tutor
Certified Tutor
All AP Calculus BC Resources























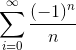


![L = \lim_{n ->\infty } \frac{a_{n+1}}{a_{n}} = \lim_{n ->\infty } \left[\left(\frac{(n+1)!}{(n+1)^2 cos (n+1)} \div \frac{n!}{n^2 cos (n) }\right)\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343419/gif.latex)















