All AP Calculus AB Resources
Example Questions
Example Question #534 : Derivatives
For the function y, at which point(s) does the rate of change in the slope shift from decreasing to increasing.



None of the other answers


For this question we want to find the points at which the second derivative of the function changes sign, i.e. 
Notice that there are two x-values at which the second derivative equals zero.
We are interested only in the point where the slope changes from decreasing to increasing, however. This means that the answer is at 
x-values less than 



Example Question #41 : Second Derivatives
On what intervals is the function 
The question is asking when the derivative is negative and the second derivative is positive. First, taking the derivative, we get
Solving for the zero's, we see 



Thus, we can see that the derivative is only negative on the interval 
Repeating the process for the second derivative,
The reader can verify that this equation hits 0 at -4/3. Thus, the intervals to test for the second derivative are

Because we want the interval where the second derivative is positive and the first derivative is negative, we need to take the intersection or overlap of the two intervals we got:

If this step is confusing, try drawing it out on a number line -- the first interval is from -3 to 1/3, the second from -4/3 to infinity. They only overlap on the smaller interval of -4/3 to 1/3.
Thus, our final answer is
Example Question #42 : Second Derivatives
On a closed interval, the function 



Two or more of the other answers are correct.




If 



For 


For 


Thus, the only correct answer is that 
Example Question #991 : Ap Calculus Ab
If
and 
then find 
We see the answer is 
Example Question #1 : Derivatives
Define 
Give the interval(s) on which 

<0)
We need to find the values of 
&space;=&space;3x%5E%7B2%7D&space;-18x+24&space;<0)
These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 

Example Question #2 : Derivatives
Define &space;=&space;x%5E%7B3%7D&space;-&space;%5Cfrac%7B21%7D%7B2%7D&space;x%5E%7B2%7D&space;+30x&space;-6)
Give the interval(s) on which 

>0)
We need to find the values of 

These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 
Example Question #1 : Derivatives
At what point does 
It does not shift from increasing to decreasing
To find out where the graph shifts from increasing to decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
If we were to graph 
Example Question #2 : Applications Of Derivatives
At what value of 

It does not shift from decreasing to increasing
To find out when the function shifts from decreasing to increasing, we look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
From here, we want to know if there is a point at which graph changes from negative to positive. Plug in zero for y and solve for x.
This is the point where the graph shifts from decreasing to increasing.
Certified Tutor
All AP Calculus AB Resources










































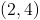
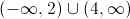

&space;=&space;3%5Ccdot&space;x%5E%7B3-1%7D&space;-2%5Ccdot&space;9x%5E%7B2-1%7D+24+0)


































































