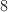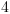Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivatives of functions

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #76 : Ap Calculus Ab

Given $f(x)=2x^{3}-7x^{2}+8x-3$ . Find f''(2) .

Possible Answers:

Correct answer:

Explanation:

First, find the first derivative.

You should get $f'(x)=6x^{2}-14x+8$ .

Next, differentiate again.

You should get f''(x)=12x-14 .

Finally, plug in x=2 to get f''(2)=10 .

Report an Error

Example Question #77 : Ap Calculus Ab

The velocity profile of a fluid is given by

$v(x)=16\cos(x)+x^2+16\sin(x)$

Determine the rate of change of the velocity of the fluid at any point.

Possible Answers:

$16(\cos(x)-\sin(x))+2x$

$16(\cos(x)-\sin(x))+x^2$

2x+16

$16(\cos(x)+\sin(x))+2x$

Correct answer:

$16(\cos(x)-\sin(x))+2x$

Explanation:

To find the rate of change of the velocity of the fluid at any point, we must take the derivative of the function:

$v'(x)=-16\sin(x)+2x+16\cos(x)=16(\cos(x)-\sin(x))+2x$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \sin(x)=\cos(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Report an Error

Example Question #78 : Ap Calculus Ab

Find :

$f=\sqrt{\tan(4x)}$

Possible Answers:

$\frac{2\sec^2(4x)}{\sqrt{\tan(4x)}}$

$\frac{1}{\sqrt{\tan(4x)}}$

$\frac{4\sec^2(4x)}{\sqrt{\tan(4x)}}$

$-\frac{2\sec^2(4x)}{\sqrt{\tan(4x)}}$

Correct answer:

$\frac{2\sec^2(4x)}{\sqrt{\tan(4x)}}$

Explanation:

The derivative of the function is equal to

$f'=\frac{1}{2}\tan(4x)^{-\frac{1}{2}}(4\sec^2(4x))=\frac{2\sec^2(4x)}{\sqrt{\tan(4x)}}$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \tan(x)=\sec^2(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Note that the chain rule was used on the square root, the inner tangent function, and the function inside the secant.

Report an Error

Example Question #79 : Ap Calculus Ab

Find the derivative of the function:

$f=\cos^2(2x)$

Possible Answers:

$-2\cos(2x)\sin(2x)$

$-4\cos(2x)\sin(2x)$

$-4\cos(4x)\sin(4x)$

$4\cos(2x)\sin(2x)$

Correct answer:

$-4\cos(2x)\sin(2x)$

Explanation:

The derivative of the function is equal to

$f'=2\cos(2x)(-2\sin(2x))=-4\cos(2x)\sin(2x)$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Notice that the chain rule was used on the cosine squared function, the cosine function, and the function inside the sine function.

Report an Error

Example Question #61 : Derivatives Of Functions

Find the derivative of the function

$f=x\cos(x^2)$

Possible Answers:

$f'=\cos(x^2)+2x^2\sin(x^2)$

$f'=-\cos(x^2)-2x^2\sin(x^2)$

$f'=\cos(x^2)-x\sin(x^2)$

$f'=\cos(x^2)-2x^2\sin(x^2)$

Correct answer:

$f'=\cos(x^2)-2x^2\sin(x^2)$

Explanation:

To find the derivative of the function, we use both the product rule and the chain rule

$f'=x'\cos(x^2)+x\cos(x^2)'=\cos(x^2)-x\sin(x^2)(2x)=\cos(x^2)-2x^2\sin(x^2)$

Report an Error

Example Question #62 : Derivatives Of Functions

Find the derivative of the function $f=\frac{x^5}{\sin(2x)}$

Possible Answers:

$f'=\frac{5x^4\sin(2x)+2x^5\cos(2x)}{\sin^2(2x)}$

$f'=\frac{5x^4\sin(2x)-2x^5\cos(2x)}{\cos^2(2x)}$

$f'=\frac{5x^4\sin(x)-2x^5\cos(2x)}{\sin^2(2x)}$

$f'=\frac{5x^4\sin(2x)-2x^5\cos(2x)}{\sin^2(2x)}$

Correct answer:

$f'=\frac{5x^4\sin(2x)-2x^5\cos(2x)}{\sin^2(2x)}$

Explanation:

To find the derivative of the function, we use both the quotient rule and the chain rule

$f'=(x^5'*\sin(2x)-x^5\sin(2x)')/\sin^2(2x))$

$f'=\frac{5x^4\sin(2x)-2x^5\cos(2x)}{\sin^2(2x)}$

Report an Error

Example Question #63 : Derivatives Of Functions

If $f(x)=\sin x$ then $f'\left({\frac{\pi }{4}}\right)=$

Possible Answers:

$\frac{{\sqrt{3}}}{2}$

$\frac{\sqrt{2}}{2}$

Correct answer:

$\frac{\sqrt{2}}{2}$

Explanation:

To calculate the derivative of this function at the desired point, first recall that,

$\sin(x)\frac{d}{dx}=\cos(x)$

$f(x)=\sin x$

$f^{'}(x)=\cos x$

Now, substitute the value into the derivative function to solve.

$f'(\frac{\pi }{4}) = cos\frac{\pi }{4} = cos(45^{\circ}) = \frac{\sqrt{2}}{2}$

Report an Error

Example Question #11 : Calculus 3

Let $f(x)=x^2-\frac{1}{1-x^2}$ . Which of the following gives the equation of the line normal to $f(x)$ when x=2 ?

Possible Answers:

$27x+111y=535$

$192x + 54y = 735$

$32x-9y=25$

$32x+9y=103$

$27x + 96y = 470$

Correct answer:

$27x + 96y = 470$

Explanation:

We are asked to find the normal line. This means we need to find the line that is perpendicular to the tangent line at x=2 . In order to find the tangent line, we will need to evaluate the derivative of f(x) at x=2 .

$f(x)=x^2-\frac{1}{1-x^2}=x^2-(1-x^2)^{-1}$

$f'(x)=2x-(-1)(1-x^2)^{-2}(-2x)$

$f'(x)=2x-2x(1-x^2)^{-2}$

$f'(2)=2(2)-2(2)(1-2^2)^{-2}$

$f'(2)=4-4(\frac{1}{9})=\frac{32}{9}$

The slope of the tangent line at x=2 is $\frac{32}{9}$ . Because the tangent line and the normal line are perpendicular, the product of their slopes must equal .

(slope of tangent)(slope of normal) =

$\left ( \frac{32}{9} \right )\cdot \left ( slope\ of\ normal \right )=-1$

$slope\ of\ normal=-\frac{9}{32}$

We now have the slope of the normal line. Once we find a point through which it passes, we will have enough information to derive its equation.

Since the normal line passes through the function at x=2 , it will pass through the point $\left ( 2,f(2) \right )$ . Be careful to use the original equation for , not its derivative.

$f(2)=2^2-(1-4)^{-1}=4-(-\frac{1}{3})=\frac{13}{3}$

The normal line has a slope of $-\frac{9}{32}$ and passes through the piont $\left ( 2,\frac{13}{3} \right )$ . We can now use point-slope form to find the equation of the normal line.

$y-\frac{13}{3}=-\frac{9}{32}(x-2)$

Multiply both sides by 32(3)=96 .

$96y-416=-27(x-2)$

$27x + 96y = 470$

The answer is $27x + 96y = 470$ .

Report an Error

Example Question #64 : Derivatives Of Functions

If the position of a particle over time is represented by $p=t^{3}-16t^{2}-7t$ then what is the particle's instantaneous acceleration at t=4 ?

Possible Answers:

Correct answer:

Explanation:

The answer is .

Since velocity is the first derivative of the position function, take the derivative once. Then, recall that the acceleration function is the second derivative of position thus the derivative needs to be taken one more time.

$p=t^{3}-16t^{2}-7t$

$velocity =p'=3t^{2}-32t-7$

$acceleration =p''=6t-32$

$p''(4)=6(4)-32 = -8$

Report an Error

Example Question #65 : Derivatives Of Functions

Consider the function:

$f(x) = -6e^{-x} + x$

The relative minimum for this function is at:

Possible Answers:

There is no relative minimum, because the first derivative is always positive.

x = 0

x = 10

None of the other answers.

$x = \frac{-1}{6}$

Correct answer:

There is no relative minimum, because the first derivative is always positive.

Explanation:

To find any relative minimum, one first needs to find the critical points by setting the first derivative equal to zero:

$f'(x) = 6e^{-x} + 1 = 0$

However, the first derivative is positive for all real values of x, since the exponential function is always positive. Thus, there are no values for which f'(x) = 0 , and therefore no critical points and no relative minimum.

Report an Error

View AP Calculus AB Tutors

Ying
Certified Tutor

Iowa State University, Master of Science, Mathematics.

View AP Calculus AB Tutors

Bertha
Certified Tutor

California Institute of Technology, Bachelor's (in progress), Chemical Engineering.

View AP Calculus AB Tutors

Lauren
Certified Tutor

Christopher Newport University, Bachelor of Science, Neuroscience. Christopher Newport University, Bachelor of Science, Psych...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Miami, Statistics Tutors in Seattle, GRE Tutors in Atlanta, Calculus Tutors in Atlanta, MCAT Tutors in Philadelphia, Physics Tutors in Miami, French Tutors in Houston, SSAT Tutors in Phoenix, SAT Tutors in Philadelphia, GMAT Tutors in Miami

Popular Courses & Classes

GMAT Courses & Classes in New York City, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Diego, ACT Courses & Classes in Boston, ACT Courses & Classes in San Diego, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Boston, LSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Denver, GRE Courses & Classes in Miami

Popular Test Prep

GMAT Test Prep in San Diego, MCAT Test Prep in San Diego, GMAT Test Prep in New York City, ACT Test Prep in San Diego, SAT Test Prep in Denver, GRE Test Prep in Boston, GRE Test Prep in Los Angeles, ACT Test Prep in Chicago, LSAT Test Prep in New York City, ACT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivatives of functions

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #76 : Ap Calculus Ab

Example Question #77 : Ap Calculus Ab

Example Question #78 : Ap Calculus Ab

Example Question #79 : Ap Calculus Ab

Example Question #61 : Derivatives Of Functions

Example Question #62 : Derivatives Of Functions

Example Question #63 : Derivatives Of Functions

Example Question #11 : Calculus 3

Example Question #64 : Derivatives Of Functions

Example Question #65 : Derivatives Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: