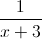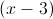Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Solving Rational Expressions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #81 : Solving Rational Expressions

Simplify: $\frac{x^2-2x}{2x}\cdot \frac{x^2}{x^2-x-2}$

Possible Answers:

$\frac{x^2}{2x+1}$

$\frac{x^2}{2x+2}$

$\frac{x}{x+2}$

$\frac{x}{2x+1}$

$\frac{x}{2x-1}$

Correct answer:

$\frac{x^2}{2x+2}$

Explanation:

Factor all the binomial and trinomial in the expression.

$\frac{x^2-2x}{2x}\cdot \frac{x^2}{x^2-x-2} = \frac{x(x-2)}{2x}\cdot \frac{x^2}{(x-2)(x+1)}$

Cancel all the common terms.

The expression becomes:

$\frac{x^2}{2(x+1)} = \frac{x^2}{2x+2}$

The answer is: $\frac{x^2}{2x+2}$

Report an Error

Example Question #25 : Multiplying And Dividing Rational Expressions

Divide: $\frac{x^2-1}{x}\div \frac{x^2}{x+1}$

Possible Answers:

$\frac{x^3+x^2-x-1}{x^2+x}$

$\frac{1}{x^2+x-1}$

x^2-x

x^2+x

$\frac{x^3+x^2-x-1}{x^3}$

Correct answer:

$\frac{x^3+x^2-x-1}{x^3}$

Explanation:

To divide this expression, take the reciprocal of the second term and change the division sign to a multiplication sign.

$\frac{x^2-1}{x}\div \frac{x^2}{x+1} = \frac{x^2-1}{x}\times \frac{x+1}{x^2} = \frac{(x^2-1)(x+1)}{x^3}$

Expand the numerator by FOIL method.

(x^2-1)(x+1) = (x^2)(x)+(x^2)(1)+(-1)(x)+(-1)(1)

x^3+x^2-x-1

Divide this by the denominator.

The answer is: $\frac{x^3+x^2-x-1}{x^3}$

Report an Error

Example Question #26 : Multiplying And Dividing Rational Expressions

Solve: $\frac{x+3}{x^2}\div\frac{x^4}{3}$

Possible Answers:

$\frac{3}{x^3+3x^2}$

$\frac{3x+9}{x^6}$

$\frac{3x+3}{x^6}$

$\frac{x^3+3x^2}{3}$

$\frac{3x+9}{x^8}$

Correct answer:

$\frac{3x+9}{x^6}$

Explanation:

In order to divide the rational expressions, we will need to convert the division sign to a multiplication sign and take the reciprocal of the second term.

$\frac{x+3}{x^2}\div\frac{x^4}{3} = \frac{x+3}{x^2} \times \frac{3} {x^4}$

Multiply the numerator with the numerator and denominator with the denominator.

3(x+3)=3x+9

x^2(x^4) = x^6

The answer is: $\frac{3x+9}{x^6}$

Report an Error

Example Question #27 : Multiplying And Dividing Rational Expressions

Divide: $\frac{3x+3}{6x-7}\div \frac{6}{x}$

Possible Answers:

$\frac{18x-18}{6x^2-7}$

$\frac{x^2+x}{12x-14}$

$\frac{x^2-x}{12x-14}$

$\frac{18x+18}{6x^2-7}$

$\frac{x^2-1}{12x-14}$

Correct answer:

$\frac{x^2+x}{12x-14}$

Explanation:

To divide the rational expression, we will need to take the reciprocal of the second term and change the division sign to a multiplication sign.

$\frac{3x+3}{6x-7}\div \frac{6}{x} = \frac{3x+3}{6x-7}\times \frac{x}{6}$

Multiply the numerator with the numerator and the denominator with the denominator.

x(3x+3) = 3x^2+3x

6(6x-7) =36x-42

Divide the numerator and denominator.

$\frac{ 3x^2+3x}{36x-42}$

Take out a three as a common factor.

$\frac{ 3x^2+3x}{36x-42}=\frac{3(x^2+x)}{3(12x-14)}=\frac{x^2+x}{12x-14}$

The answer is: $\frac{x^2+x}{12x-14}$

Report an Error

Example Question #28 : Multiplying And Dividing Rational Expressions

Divide: $\frac{x^3-1}{x+1} \div \frac{1}{x-1}$

Possible Answers:

$\frac{x^2+x+1}{x+1}$

$\frac{x^2+1}{x-1}$

$\frac{x^4-x^3-x+1}{x+1}$

$\frac{x^2+x+1}{x-1}$

$\frac{x^4+x^3+x+1}{x+1}$

Correct answer:

$\frac{x^4-x^3-x+1}{x+1}$

Explanation:

Be very careful not to apply the difference of cubes to simplify this expression!

Change the sign to multiplication and take the reciprocal of the second term.

$\frac{x^3-1}{x+1} \div \frac{1}{x-1}=\frac{x^3-1}{x+1} \cdot\frac{ x-1}{1}$

Multiply the top by FOIL method.

(x^3-1)(x-1) = (x^3)(x)+(x^3)(-1)+(-1)(x)+(-1)(-1)

x^4-x^3-x+1

Divide this by the denominator.

The answer is: $\frac{x^4-x^3-x+1}{x+1}$

Report an Error

Example Question #29 : Multiplying And Dividing Rational Expressions

Simplify: $\frac{x}{x-9}\div\frac{x-9}{x-18}$

Possible Answers:

$\frac{x^2-18}{x^2-18+81}$

$\frac{x+2}{x-9}$

$\frac{x}{x-18}$

$\frac{x+9}{x^2-18+81}$

$\frac{x-18}{x}$

Correct answer:

$\frac{x^2-18}{x^2-18+81}$

Explanation:

In order to simplify the rational expression, we will need to rewrite the expression as a multiplication sign and take the reciprocal of the second term.

$\frac{x}{x-9}\div\frac{x-9}{x-18}= \frac{x}{x-9} \times \frac{x-18}{x-9}$

Simplify the numerator.

x(x-18) = x^2-18x

Simplify the denominator by FOIL method.

(x-9)(x-9)= x^2-9x-9x+81 = x^2-18x+81

Divide the numerator with the denominator.

The answer is: $\frac{x^2-18}{x^2-18+81}$

Report an Error

Example Question #22 : Multiplying And Dividing Rational Expressions

Simplify: $\frac{x^2-x}{x^3-x} \cdot \frac{x+1}{x-1}$

Possible Answers:

$\frac{x}{x+1}$

$\frac{1}{x-1}$

$\frac{x}{x-1}$

$\frac{1}{x^2-1}$

Correct answer:

$\frac{1}{x-1}$

Explanation:

Rewrite the left fraction using common factors.

$\frac{x^2-x}{x^3-x} \cdot \frac{x+1}{x-1} = \frac{x(x-1)}{x(x^2-1)} \cdot \frac{x+1}{x-1}$

Cancel out common terms.

$\frac{x+1}{x^2-1}$

Factorize the bottom term.

$\frac{x+1}{x^2-1} =\frac{x+1}{(x+1)(x-1)} = \frac{1}{x-1}$

The answer is: $\frac{1}{x-1}$

Report an Error

Example Question #31 : Multiplying And Dividing Rational Expressions

Evaluate: $\frac{x^2}{x-2}\cdot \frac{3x}{8}$

Possible Answers:

$\frac{3x^3}{8x-16}$

$\frac{8x}{3x-6}$

$\frac{3x^3}{8x-2}$

$\frac{3x^2}{8x-16}$

$\frac{3x^2}{8x-2}$

Correct answer:

$\frac{3x^3}{8x-16}$

Explanation:

To multiply a rational expression, simplify multiply the numerator with the numerator, and the denominator with the denominator.

$\frac{x^2}{x-2}\cdot \frac{3x}{8} = \frac{3x(x^2)}{8(x-2)}$

Simplify the top and bottom by distribution.

$\frac{3x^3}{8x-16}$

This can no longer be simplified.

The answer is: $\frac{3x^3}{8x-16}$

Report an Error

Example Question #81 : Solving Rational Expressions

Simplify:

$\frac{x+3}{x^{2}+6x+9}$

Possible Answers:

$\left ( x-3 \right )$

$\frac{1}{\left ( x+3 \right )^{2}}$

$\left ( x+3 \right )^{2}$

$\frac{1}{x+3}$

$\left ( x+3 \right )$

Correct answer:

$\frac{1}{x+3}$

Explanation:

If we factors the denominator we get

$\left ( x+3 \right )^{2}$

Hence the rational expression becomes equal to

$\frac{\left ( x+3 \right )}{\left ( x+3 \right )^{2}}$

which is equal to $\frac{1}{\left ( x+3 \right )}$

Report an Error

Example Question #2 : Factoring Rational Expressions

Simplify.

$\frac{2x^2-4x-6}{4x-12}$

Possible Answers:

$\frac{x+1}{2}$

$\frac{x^2-2x-3}{2(x-3)}$

The expression cannot be simplified.

x+1

2x+2

Correct answer:

$\frac{x+1}{2}$

Explanation:

a. Simplify the numerator and denominator separately by pulling out common factors.

$\frac{2(x^2-2x-3)}{4(x-3)}$

b. Reduce if possible.

$\frac{x^2-2x-3}{2(x-3)}$

c. Factor the trinomial in the numerator.

$\frac{(x-3)(x+1)}{2(x-3)}$

d. Cancel common factors between the numerator and the denominator.

$\frac{{\color{Red} (x-3)}(x+1)}{2{\color{Red} (x-3)}}=\frac{x+1}{2}$

Report an Error

View Algebra 2 Tutors

Daniel
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Psychology.

View Algebra 2 Tutors

Aaron
Certified Tutor

Austin Peay State University, Bachelor, Education.

View Algebra 2 Tutors

Akshar
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Computer and Information Sciences, General.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Miami, Statistics Tutors in Seattle, LSAT Tutors in Seattle, Statistics Tutors in Denver, LSAT Tutors in Philadelphia, Statistics Tutors in Miami, Biology Tutors in Dallas Fort Worth, Biology Tutors in Philadelphia, Chemistry Tutors in Dallas Fort Worth, Computer Science Tutors in Seattle

Popular Courses & Classes

ACT Courses & Classes in Boston, GRE Courses & Classes in Philadelphia, SAT Courses & Classes in San Diego, Spanish Courses & Classes in Chicago, Spanish Courses & Classes in Miami, SAT Courses & Classes in Houston, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Miami

Popular Test Prep

MCAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Philadelphia, ACT Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in New York City, LSAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Miami, LSAT Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Solving Rational Expressions

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #81 : Solving Rational Expressions

Example Question #25 : Multiplying And Dividing Rational Expressions

Example Question #26 : Multiplying And Dividing Rational Expressions

Example Question #27 : Multiplying And Dividing Rational Expressions

Example Question #28 : Multiplying And Dividing Rational Expressions

Example Question #29 : Multiplying And Dividing Rational Expressions

Example Question #22 : Multiplying And Dividing Rational Expressions

Example Question #31 : Multiplying And Dividing Rational Expressions

Example Question #81 : Solving Rational Expressions

Example Question #2 : Factoring Rational Expressions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: