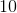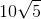Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Circle Functions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Quadratic Functions

Determine the center and radius, respectively, given the equation:

x^2+y^2 +6x-2y-2 = 0

Possible Answers:

$(-3,1); 3\sqrt2$

$(3,-1); 2\sqrt3$

(-3,1); 144

$(-3,1); 2\sqrt3$

(3,-1); 144

Correct answer:

$(-3,1); 2\sqrt3$

Explanation:

In order to solve for the radius, we will need to complete the square twice.

Group the x and y-variables in parentheses. Starting from the original equation:

x^2+y^2 +6x-2y-2 = 0

(x^2+6x)+(y^2-2y)-2 = 0

Add two on both sides.

(x^2+6x)+(y^2-2y)=2

Divide by the second term coefficient of each binomial by 2, and add the squared quantity on both sides of the equation.

$(x^2+6x+(\frac{6}{2})^2)+(y^2-2y+(\frac{-2}{2})^2) = 2+(\frac{6}{2})^2+(\frac{-2}{2})^2$

The equation becomes:

(x^2+6x+9)+(y^2-2y+1)=2+9+1

Factorize both polynomials in parentheses and simplify the right side.

(x+3)^2+(y-1)^2 =12

The center is: (h,k)= (-3,1)

The radius is: $r=\sqrt{12}=2\sqrt3$

The answer is: $(-3,1); 2\sqrt3$

Report an Error

Example Question #1 : Graphing Circle Functions

Determine the graph of the equation

4(x-2)^2+4(y-3)^2=1

Possible Answers:

Hyperbola, centered at (2,3)

Circle, centered at (2,3) with radius r= 1/2

Circle, centered at (2,3) with radius r= 1/4

Ellipse, centered at (2,3)

Correct answer:

Circle, centered at (2,3) with radius r= 1/2

Explanation:

The equation of a circle in standard for is:

(x-h)^2+(y-k)^2=r^2

Where the center (x,y)=(h,k) and the radius of the cirlce is .

Dividing by 4 on both sides of the equation yields

$(x-2)^2+(y-3)^2 = \frac{1}{4}$

$(x-2)^2+(y-3)^2 = \bigg(\frac{1}{2}\bigg)^2$

an equation whose graph is a circle, centered at (2,3) with radius = .5

Report an Error

Example Question #2 : Graphing Circle Functions

Give the radius and the center of the circle for the equation below.

$(x-3)^{2}+(y + 4)^2 = 16$

Possible Answers:

r = 16

$\text{Center} = (3, 4)$

r = 4

$\text{Center} = (3, 4)$

r = 4

$\text{Center} = (-3, 4)$

r = 16

$\text{Center} = (3, -4)$

r = 4

$\text{Center} = (3, -4)$

Correct answer:

r = 4

$\text{Center} = (3, -4)$

Explanation:

Look at the formula for the equation of a circle below.

$(x - h)^{2}+(y -k)^{2} = r^{2}$

Here (h, k) is the center and is the radius. Notice that the subtraction in the center is part of the formula. Thus, looking at our equation it is clear that the center is (3, -4) and the radius squared is . When we square root this value we get that the radius must be .

Report an Error

Example Question #1 : Graphing Circle Functions

Determine the equation of a circle whose center lies at the point $\left ( 3,4\right )$ and has a radius of .

Possible Answers:

(x-3)^2+(y-4)^2=1

$\frac{x^2}{3}+\frac{y^2}{4}-1=0$

$\frac{x^2}{3}-\frac{y^2}{4}=1$

(x+3)^2+(y+4)^2=1

Correct answer:

(x-3)^2+(y-4)^2=1

Explanation:

The equation for a circle with center (h,k) and radius is :

(x-h)^2+(y-k)^2=r^2

Our circle is centered at (3,4) with radius r=1 , so the equation for this circle is :

(x-3)^2+(y-4)^2=1

Report an Error

Example Question #1 : Graphing Circle Functions

$\small f(x)=(x-2)^2+(y+5)^2=36$

What is the radius of the circle?

Possible Answers:

$\small \small r=5$

$\small \small r=3$

$\small \small r=36$

$\small \small r=2$

$\small r=6$

Correct answer:

$\small r=6$

Explanation:

The parent equation of a circle is represented by $\small f(x)=(x-h)^2+(y-k)^2=r^2$ . The radius of the circle is equal to $\small r$ . The radius of the cirle is $\small \sqrt{36}$ .

Report an Error

Example Question #5 : Graphing Circle Functions

What is the center of the circle expressed by the funciton $\small x^2+4x+y^2=5$ ?

Possible Answers:

$\small (0,0)$

$\small (-5,0)$

$\small (-2,0)$

$\small (5,0)$

$\small (2,0)$

Correct answer:

$\small (-2,0)$

Explanation:

The equation can be rewritten so that it looks like the parent equation for a circle $\small (x-h)^2+(y-k)^2=r^2$ . After completeing the square, the equation changes from $\small x^2+4x+y^2=5$ to $\small x^2+4x+4+y^2=9$ . From there it can be expressed as $\small (x+2)^2+y^2=9$ . Therefore the center of the circle is at $\small (-2,0)$ .

Report an Error

Example Question #2 : Graphing Circle Functions

The graph of the equation

$x^{2} + y^{2} + 10x - 8y = 84$

is a circle with what as the length of its radius?

Possible Answers:

$5\sqrt{5}$

$10\sqrt{5}$

Correct answer:

$5\sqrt{5}$

Explanation:

Rewrite the equation of the circle in standard form

$(x - h)^{2} + \left ( y - k\right )^{2} = r^{2}$

as follows:

$x^{2} + y^{2} + 10x - 8y = 84$

$x^{2} + 10x+ y^{2} - 8y = 84$

Since $\left (\frac{10}{2} \right ) ^{2} = 5 ^{2} = 25$ and $\left (\frac{-8}{2} \right ) ^{2} = (-4)^{2} = 16$ , we complete the squares by adding:

$x^{2} + 10x+ 25 + y^{2} - 8y + 16 = 84 + 25 + 16$

$(x+5) ^{2} + \left (y- 4 \right ) ^{2} = 125$

The standard form of the equation sets

$r^{2} = 125$ ,

so the radius of the circle is

$r = \sqrt{125} = \sqrt{25} \cdot \sqrt{5} = 5 \sqrt{5}$

Report an Error

Example Question #1 : Graphing Circle Functions

What are the coordinates of the center of a circle with the equation (x - 1)^2 + (y - 6)^2 = 25 ?

Possible Answers:

(-1, -6)

(1, 6)

(-6, -1)

(6, 1)

Correct answer:

(1, 6)

Explanation:

The equation of a circle is (x - h)^2 + (y - k)^2 = r^2 , in which (h, k) is the center of the circle. To derive the center of a circle from its equation, identify the constants immediately following x and y, and flip their signs. In the given equation, x is followed by -1 and y is followed by -6, so the coordinates of the center must be (1, 6).

Report an Error

Example Question #8 : Graphing Circle Functions

What is the radius of a circle with the equation x^2 + 6x + y^2 + 2y = -6 ?

Possible Answers:

Correct answer:

Explanation:

To convert the given equation into the format (x - h)^2 + (y - k)^2 = r^2 , complete the square by adding (b/2a)^2 to the x-terms and to the y-terms.

x^2 + 6x + y^2 + 2y = -6

x^2 + 6x + (6/2)^2 + y^2 + 2y + (2/2)^2 = -6 + (6/2)^2 + (2/2)^2

x^2 + 6x + 9 + y^2 + 2y + 1 = -6 + 9 + 1

(x + 3)^2 + (y + 1)^2 = 4

The square root of 4 is 2, so the radius of the circle is 2.

Report an Error

Example Question #9 : Graphing Circle Functions

What is the radius of a circle with the equation x^2 + 8x + y^2 - 4y = 5 ?

Possible Answers:

Correct answer:

Explanation:

To convert the given equation into the format (x - h)^2 + (y - k)^2 = r^2 , complete the square by adding (b/2a)^2 to the x-terms and to the y-terms.

x^2 + 8x + y^2 - 4y = 5

x^2 + 8x + (8/2)^2 + y^2 - 4y + (-4/2)^2 = 5 + (8/2)^2 + (-4/2)^2

x^2 + 8x + 16 + y^2 - 4y + 4 = 5 + 16 + 4

(x + 4)^2) + (y - 2)^2 = 25

The square root of 25 is 5, so the radius of the circle is 5.

Report an Error

View Algebra 2 Tutors

Chelsea
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Physics. The University of Texas at Dallas, Master of Science, Bioinf...

View Algebra 2 Tutors

Rachel
Certified Tutor

Grand Canyon University, Bachelor of Science, Mathematics Teacher Education. Grand Canyon University, Master of Science, Addi...

View Algebra 2 Tutors

Samantha
Certified Tutor

Middlesex County College, Associate in Science, Sustainability Studies.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Philadelphia, LSAT Tutors in New York City, MCAT Tutors in Los Angeles, Computer Science Tutors in San Francisco-Bay Area, ISEE Tutors in Atlanta, French Tutors in Atlanta, MCAT Tutors in Philadelphia, Math Tutors in Los Angeles, LSAT Tutors in Chicago, MCAT Tutors in Seattle

Popular Courses & Classes

GMAT Courses & Classes in Seattle, ISEE Courses & Classes in Chicago, MCAT Courses & Classes in Miami, LSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Atlanta, LSAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Atlanta, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Atlanta, SSAT Courses & Classes in Houston

Popular Test Prep

ACT Test Prep in Philadelphia, SSAT Test Prep in Seattle, MCAT Test Prep in Denver, ACT Test Prep in San Diego, ACT Test Prep in Denver, MCAT Test Prep in Washington DC, SSAT Test Prep in Phoenix, SSAT Test Prep in San Diego, SAT Test Prep in Denver, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Circle Functions

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #61 : Quadratic Functions

Example Question #1 : Graphing Circle Functions

Example Question #2 : Graphing Circle Functions

Example Question #1 : Graphing Circle Functions

Example Question #1 : Graphing Circle Functions

Example Question #5 : Graphing Circle Functions

Example Question #2 : Graphing Circle Functions

Example Question #1 : Graphing Circle Functions

Example Question #8 : Graphing Circle Functions

Example Question #9 : Graphing Circle Functions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: