Algebra 1 : Algebra 1
Study concepts, example questions & explanations for Algebra 1
All Algebra 1 Resources
Example Questions
Example Question #1 : How To Write Expressions And Equations
Translate this sentence into a mathematical equation:
Three less than five times a number is the same as two more than twice that number.
Three less than five times a number is the same as two more than twice that number.
Let the number be 
"Three less than five times a number" translates into 
"Is the same as" means equal to or "
"Two more than twice that number" means 
Putting these together gives:
Example Question #3 : How To Write Expressions And Equations
For the given equation determine the slope:
By changing the equation to slope intercept form we get the following:
Hence the slope is
Example Question #7 : How To Write Expressions And Equations
What is the slope and the 
slope = undefined, x-int = -3, y-int = none
slope = 0, x-int = -3, y-int = 2
slope = undefined, x-int 2, y-int = -3
slope = 1, x-int = 2, y-int = 2
slope = 0, x-int = 2, y-int = -3
slope = undefined, x-int = -3, y-int = none
For a vertical line e.g. 
This line does not intersect the 
Since the line passes through 
Example Question #6 : How To Write Expressions And Equations
Write the equation of a line with a slope of
and passes through the point 
Here we use the point-slope formula of a line which is
By plugging in 
which is equal to
When the above is simplified we get:
Example Question #1 : How To Write Expressions And Equations
Complete the missing information for the equation of the following line
and determine which one of the 
Replacing 
Example Question #2 : How To Write Expressions And Equations
Convert the following into the standard form of a line:
Multiplying each term of the given equation by the denominator of the slope which is 5 one gets :
which can be written as
Example Question #921 : Algebra 1
Equations of a line can be represented as follows:
(1) 
(2) 
(3) 
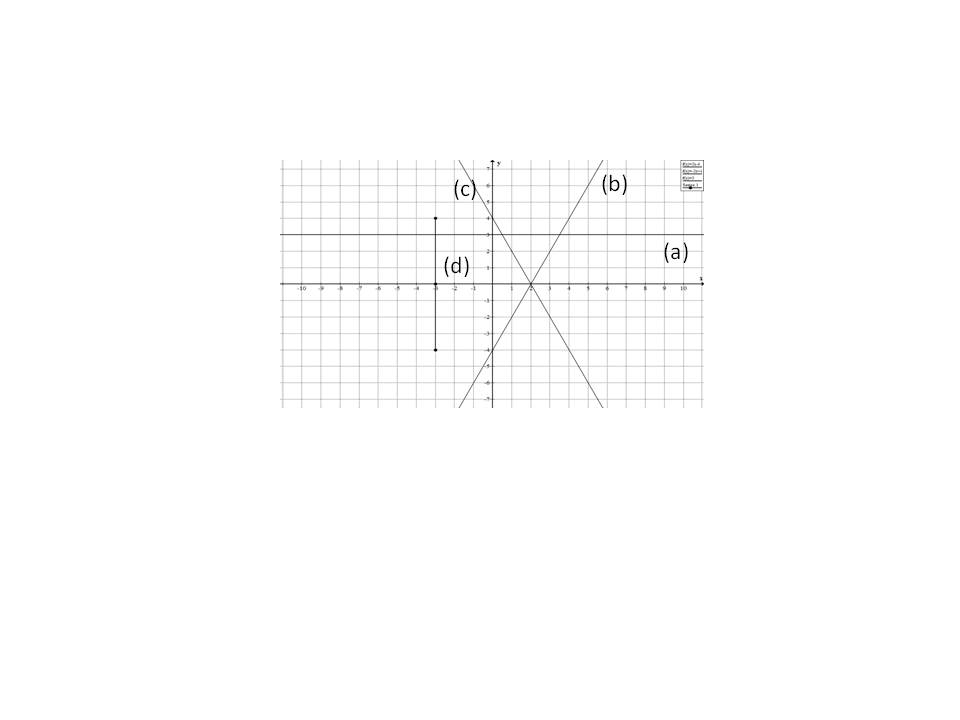
none of the above
The equation of line 
Hence
and the
Example Question #922 : Algebra 1
Find the equation of a line parallel to
and passes through 
The equation of a line parallel to the given line must be of the form:
Since the line passes through 
we can calculate 
Solving for 
Example Question #923 : Algebra 1
Find the equation of a line perpendicular to
and passes through
The slope of a line perpendicular to
which has a slope of 
Hence we get
Replacing 
Solving for 
Example Question #11 : How To Write Expressions And Equations
Find the equation of a line perpendicular to
and passes through
Any line perpendicular to 
which is a horizontal line, must be a vertical line.
Since it passes through the point 
The equation must be
All Algebra 1 Resources
