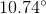We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Circles

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Length Of An Arc

If a circle has a circumference of , what is the measure of the arc contained by a degree angle located at the center of the circle?

Possible Answers:

$4\pi$

4.8

Correct answer:

Explanation:

A circle has a total of 360 degrees. If our angle is located at the center and is degrees, we can do $\frac{60}{360}=\frac{1}{6}$ to see that our angle makes up $\frac{1}{6}$ of the complete circle.

Therefore, our arc is going to be $\frac{1}{6}$ of our total circumference. $24\cdot \frac{1}{6}=\frac{24}{6}=4$

Report an Error

Example Question #3 : How To Find The Length Of An Arc

What is the area of the sector of a circle with a central angle of 120 degrees and a radius of 5cm ? Simplify any fractions and leave your answer in terms of $\pi$ .

Possible Answers:

$\frac{3\pi}{25}cm^2$

$24\pi cm^2$

$3000\pi cm^2$

$25\pi \cm^2$

$\frac{25\pi}{3} cm^2$

Correct answer:

$\frac{25\pi}{3} cm^2$

Explanation:

The formula for the area of a sector of a circle is:

$\frac{central\: angle}{360}*\pi r^2$

The central angle given is 120 thus:

$\frac{120}{360}*\pi (5cm)^2= \frac{1}{3}\pi 25cm^2 = \frac{25\pi}{3}cm^2$

Report an Error

Example Question #51 : Circles

A water wheel turns a $120^{\circ}$ arc every minute. If the radius of the wheel is , how far in meters does the wheel turn along its edge each minute?

Possible Answers:

$\frac{5\pi}{3} m$

$8\pi m$

$10\pi m$

$\frac{\pi}{3} m$

$4\pi m$

Correct answer:

$4\pi m$

Explanation:

If the radius is , then the circumference of the wheel is:

$C = 2r\pi = 12\pi$

If the wheel turns $120^{\circ}$ each minute, then it turns $\frac{120^{\circ}}{360^{\circ}} = \frac{1}{3}$ of the circumference each minute.

$d = 12\pi \cdot \frac{1}{3} = 4\pi$

Thus, the wheel turns $4\pi m$ each minute.

Report an Error

Example Question #4 : How To Find The Length Of An Arc

What is the length of the arc ABC ?

arc2

The total area of the circle is $64\pi \, in^{2}$ and the area of the shaded region is $12\pi \,in^{2}$ .

Possible Answers:

$8\:in$

$\frac{12\pi}{5}\:in$

$\frac{3\pi}{16}\:in$

$16\pi\:in$

$3\pi\:in$

Correct answer:

$3\pi\:in$

Explanation:

If the area of the circle is $64\pi\:in^2$ , the radius can be found using the formula for the area of a circle:
$A=\pi r^2$

For our data, this is:

$64\pi=\pi r^2$

r^2=64

Therefore, $r=8\:in$

Now, the circumference of the circle is defined as:

$C=2\pi r$

For our data, this is:

$C=2*8*\pi=16\pi\:in$

Now, we know that a sector is a percentage of the total area. This percentage is easily calculated:

$\frac{12\pi\:in^2}{64\pi\:in^2}=\frac{3}{16}$

So, the length of the arc will merely be the same percentage, but now applied to the circumference:

$\frac{3}{16} * 16\pi\:in = 3\pi\:in$

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

Circle

In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?

Possible Answers:

cannot be determined

100

Correct answer:

Explanation:

Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.

Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.

Report an Error

Example Question #2 : How To Find The Angle Of A Sector

What is the angle of a sector of area in^2 on a circle having a radius of $15\:in$ ?

Possible Answers:

$3.00^{\circ}$

$22.92^{\circ}$

$0.06^{\circ}$

$15.22^{\circ}$

$72.00^{\circ}$

Correct answer:

$22.92^{\circ}$

Explanation:

To begin, you should compute the complete area of the circle:

$A=\pi r^2$

For your data, this is:

$A=15^2\pi=225\pi$

Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:

$\frac{45}{225\pi}$

Now, multiply this by the total 360 degrees in a circle:

$\frac{45}{225\pi}*360=22.918311805212$

Rounded, this is $22.92^{\circ}$ .

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

What is the angle of a sector that has an arc length of 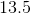13.5 on a circle of diameter ?

Possible Answers:

$10.74^{\circ}$

$128.92^{\circ}$

$14.24^{\circ}$

$35.81^{\circ}$

$194.14^{\circ}$

Correct answer:

$128.92^{\circ}$

Explanation:

The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:

$C=\pi d$

For your data, this means,

$C=12\pi$

Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:

$\frac{13.5}{12\pi}*360=128.9155039044336$

Rounded to the nearest hundredth, this is $128.92^{\circ}$ .

Report an Error

Example Question #2 : Diameter

The perimeter of a circle is 36 π. What is the diameter of the circle?

Possible Answers:

Correct answer:

Explanation:

The perimeter of a circle = 2 πr = πd

Therefore d = 36

Report an Error

Example Question #51 : Circles

Two legs of a right triangle measure 3 and 4, respectively. What is the area of the circle that circumscribes the triangle?

Possible Answers:

$12.5\pi$

$25\pi$

$6\pi$

$6.25\pi$

$5\pi$

Correct answer:

$6.25\pi$

Explanation:

For the circle to contain all 3 vertices, the hypotenuse must be the diameter of the circle. The hypotenuse, and therefore the diameter, is 5, since this must be a 3-4-5 right triangle.

The equation for the area of a circle is A = πr².

$A=\pi (5/2)^2=6.25\pi$

Report an Error

Example Question #1 : Diameter

If a circle has an area of $49\pi$ , what is the diameter of the circle?

Possible Answers:

3.5

Correct answer:

Explanation:

1. Use the area to find the radius:

$Area=\pi r^{2}$

$49\pi=\pi r^{2}$

$49=r^{2}$

r=7

2. Use the radius to find the diameter:

$d=2r=2\cdot 7=14$

Report an Error

View ACT Math Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View ACT Math Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

Spanish Courses & Classes in Houston, GRE Courses & Classes in Chicago, ACT Courses & Classes in Boston, SSAT Courses & Classes in Denver, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Atlanta, ACT Courses & Classes in Phoenix

Popular Test Prep

GMAT Test Prep in Miami, SSAT Test Prep in Seattle, LSAT Test Prep in Philadelphia, LSAT Test Prep in Atlanta, ACT Test Prep in Phoenix, SSAT Test Prep in Miami, ISEE Test Prep in Boston, ISEE Test Prep in Los Angeles, GMAT Test Prep in Phoenix, SAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Circles

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : How To Find The Length Of An Arc

Example Question #3 : How To Find The Length Of An Arc

Example Question #51 : Circles

Example Question #4 : How To Find The Length Of An Arc

Example Question #1 : How To Find The Angle Of A Sector

Example Question #2 : How To Find The Angle Of A Sector

Example Question #1 : How To Find The Angle Of A Sector

Example Question #2 : Diameter

Example Question #51 : Circles

Example Question #1 : Diameter

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: