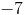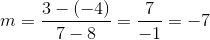We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Other Lines

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find Slope Of A Line

What is the slope of the line represented by the equation $6y-16x=7$ ?

Possible Answers:

$\frac{7}{6}$

$16$

$6$

$\frac{8}{3}$

$-16$

Correct answer:

$\frac{8}{3}$

Explanation:

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Report an Error

Example Question #221 : Geometry

What is the slope of the given linear equation?

2x + 4y = -7

Possible Answers:

1/2

-7/2

-1/2

-2

Correct answer:

-1/2

Explanation:

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Report an Error

Example Question #1423 : Gre Quantitative Reasoning

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Possible Answers:

$\frac{1}{28}$

$-\frac{1}{28}$

Correct answer:

Explanation:

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Report an Error

Example Question #1 : How To Find The Slope Of A Line

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Possible Answers:

$\frac{1}{2}$

$4$

$\frac{2}{3}$

$-\frac{1}{2}$

$-\frac{2}{3}$

Correct answer:

$\frac{1}{2}$

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Report an Error

Example Question #2 : How To Find The Slope Of A Line

What is the slope of a line running through points (7,3) and (8,-4) ?

Possible Answers:

$-\frac{1}{7}$

$\frac{7}{3}$

Correct answer:

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Report an Error

Example Question #4 : How To Find The Slope Of A Line

What is the slope of the line defined as 3x + 4y = 22 ?

Possible Answers:

$\frac{-2}{11}$

$\frac{-4}{3}$

$\frac{11}{2}$

$\frac{-3}{4}$

$\frac{4}{3}$

Correct answer:

$\frac{-3}{4}$

Explanation:

3x + 4y = 22

To calculate the slope of a line from an equation of the line, the easiest way to proceed is to solve it for . This will put it into the format y=mx+b , making it very easy to find the slope . For our equation, it is:

4y = 22-3x or 4y = -3x+22

Next you merely need to divide by :

$y = \frac{-3}{4}x+\frac{22}{4}$

Thus, the slope is $\frac{-3}{4}$

Report an Error

Example Question #91 : Algebra

What is the slope of the line perpendicular to 4x + 2y = 88 ?

Possible Answers:

$\frac{44}{3}$

$\frac{1}{2}$

$\frac{-1}{11}$

Correct answer:

$\frac{1}{2}$

Explanation:

To begin, it is easiest to find the slope of a line by putting it into the form y=mx+b . is the slope, so you can immediately find this once you have the format correct. Thus, solve our equation for :

2y = 88-4x

y = -2x +44

Now, recall that perpendicular lines have slopes of opposite sign and reciprocal numerical value. Thus, if our slope is , its perpendicular paired line will have a slope of $\frac{1}{2}$ .

Report an Error

Example Question #96 : Algebra

What is the slope of the line defined by the equation 3x + 5y = y + 20 ?

Possible Answers:

$\frac{4}{3}$

$\frac{1}{3}$

$-\frac{3}{4}$

Correct answer:

$-\frac{3}{4}$

Explanation:

The easiest way to find the slope of a line based on its equation is to put it into the form y=mx+b . In this form, you know that is the slope.

Start with your original equation 3x + 5y = y + 20 .

Now, subtract from both sides:

3x + 4y = 20

Next, subtract from both sides:

4y = 20-3x

Finally, divide by :

$y = 5-\frac{3}{4}x$

This is the same as:

$y = -\frac{3}{4}x + 5$

Thus, the slope is $-\frac{3}{4}$ .

Report an Error

Example Question #97 : Algebra

What is the slope of the line represented by the equation 4y - 5 = 12x ?

Possible Answers:

1/3

-5/12

Correct answer:

Explanation:

The slope of an equation can be calculated by simplifying the equation to the slope-intercept form y = mx + b , where m=slope.

Since 4y - 5 = 12x , we can solve for y. In shifting the 5 to the other side, we are left with 4y = 12x + 5 .

This can be further simplified to

$y = 3x + \frac{5}{4}$ , leaving us with the y = mx + b slope intercept form.

In this scenario, m=3 , so slope .

Report an Error

Example Question #221 : Geometry

Find the slope of the line 6X – 2Y = 14

Possible Answers:

-3

-6

Correct answer:

Explanation:

Put the equation in slope-intercept form:

y = mx + b

-2y = -6x +14

y = 3x – 7

The slope of the line is represented by M; therefore the slope of the line is 3.

Report an Error

View ACT Math Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View ACT Math Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Miami, Spanish Courses & Classes in Denver, SAT Courses & Classes in Miami, GRE Courses & Classes in Houston, MCAT Courses & Classes in Seattle, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Houston, GMAT Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in San Diego, LSAT Test Prep in Boston, ACT Test Prep in Miami, ISEE Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, ISEE Test Prep in Seattle, GRE Test Prep in Denver, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Philadelphia, SAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Other Lines

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #11 : How To Find Slope Of A Line

Example Question #221 : Geometry

Example Question #1423 : Gre Quantitative Reasoning

Example Question #1 : How To Find The Slope Of A Line

Example Question #2 : How To Find The Slope Of A Line

Example Question #4 : How To Find The Slope Of A Line

Example Question #91 : Algebra

Example Question #96 : Algebra

Example Question #97 : Algebra

Example Question #221 : Geometry

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: