Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Quadratic Equations

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Quadratic Equations

Solve for :

x^2 + 4x + 24 = 6 - 5x

Round to the nearest hundredth.

Possible Answers:

$-4.44\textup{ and }2.41$

$-6\textup{ and}-3$

$\textup{No solution}$

$6\textup{ and }3$

$4.44\textup{ and}-2.41$

Correct answer:

$-6\textup{ and}-3$

Explanation:

With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to :

Thus, simplify x^2 + 4x + 24 = 6 - 5x into:

x^2 + 9x + 18 = 0

Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it can. Factor the quadratic expression:

(x+3)(x+6)=0

Now, remember that you merely need to set each group equal to . This gives you the two values for :

x+3=0 ; therefore x=-3

Likewise, for the other group, x=-6

Report an Error

Example Question #52 : Quadratic Equations

Solve for :

2x^2 + 19x + 10 = 4 - x^2

Possible Answers:

$3\textup{ and }6$

$\frac{2}{5}\textup{ and }\frac{4}{5}$

$\frac{1 + \sqrt{6}}{3}\textup{ and }\frac{1 - \sqrt{6}}{3}$

$\textup{No solution}$

$-6\textup{ and }\frac{-1}{3}$

Correct answer:

$-6\textup{ and }\frac{-1}{3}$

Explanation:

With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to :

Thus, simplify 2x^2 + 19x + 10 = 4 - x^2 into:

3x^2 + 19x + 6 = 0

Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it can, though we are sometimes a bit intimidated by x^2 terms that have a coefficient like this. Factor the quadratic expression:

(3x+1)(x+6)=0

If you FOIL this out, you will see your original equation.

Now, remember that you merely need to set each group equal to . This gives you the two values for :

3x+1=0

3x=-1

$x=\frac{-1}{3}$

For the other group, you get x=-6 .

Report an Error

Example Question #305 : Equations / Inequalities

Solve for :

x^2 + 16x - 5 = 10 - 4x

Possible Answers:

$\frac{-20 \pm \sqrt{14}}{2}$

$-10\pm\sqrt{115}$

$-30\textup{ and }30$

$\textup{No solution}$

$\frac{-20 \pm \sqrt{30}}{2}$

Correct answer:

$-10\pm\sqrt{115}$

Explanation:

With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to :

Thus, simplify x^2 + 16x - 5 = 10 - 4x into:

x^2 + 20x - 15 = 0

Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it cannot be easily factored. Therefore, you should use the quadratic formula. Recall that its general form is:

$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

For our data, a=1 , b=20 , and c=-15 .

Thus, we have:

$\frac{-20\pm\sqrt{20^2-(4*1*-15)}}{2*1}$

Simplifying, this is:

$\frac{-20\pm\sqrt{400-(-60)}}{2}$

$\frac{-20\pm\sqrt{400+60}}{2}$

$\frac{-20\pm\sqrt{460}}{2}$

Now, simplify.

$\frac{-20\pm\sqrt{2*2*5*23}}{2}=\frac{-20\pm2\sqrt{115}}{2}=-10\pm\sqrt{115}$

Report an Error

Example Question #306 : Equations / Inequalities

Solve for :

7x^2 + 3x +25 = 4x - 10

Possible Answers:

$\frac{-5 \pm \sqrt{31}}{3}$

$\frac{1 \pm \sqrt{491}}{-2}$

$-8.5\textup{ and}-3.5$

$\textup{No real solution}$

$-12\textup{ and }4$

Correct answer:

$\textup{No real solution}$

Explanation:

With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to :

Thus, simplify 7x^2 + 3x +25 = 4x - 10 into:

7x^2 -x +35 = 0

$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

For our data, a=7 , b=-1 , and c=35 .

Thus, we have:

$\frac{-(-1)\pm\sqrt{(-1)^2-(4*7*35)}}{2*-1}$

Simplifying, this is:

$\frac{1\pm\sqrt{1-(980)}}{-2}$

Since 1-980 is negative, you know that there is no real solution (given the problems arising from the negative square root)!

Report an Error

Example Question #51 : Quadratic Equations

Solve: 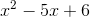$x^{2}-5x+6$

Possible Answers:

None of the other answers

and

Correct answer:

and

Explanation:

To solve, we must set it equal to zero. The above expression is of the form $ax^{2}+bx+c$ , so we can use the quadratic formula:

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

to solve for the roots which are and

We can check by plugging the roots into the expression and making sure that it equals zero.

Report an Error

View ACT Math Tutors

Marie
Certified Tutor

Silliman University, Master of Science, Mathematics.

View ACT Math Tutors

David
Certified Tutor

The University of Texas at El Paso, Bachelor of Science, Computational Mathematics. Indiana State University, Master of Scien...

View ACT Math Tutors

Alejandro
Certified Tutor

Kennesaw State University, Bachelor of Science, Computer Software Engineering.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Atlanta, LSAT Courses & Classes in Houston, SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Washington DC, LSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Houston, SAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Chicago, ISEE Test Prep in San Diego, SAT Test Prep in Miami, ISEE Test Prep in Boston, GRE Test Prep in Houston, LSAT Test Prep in Philadelphia, ACT Test Prep in Houston, ISEE Test Prep in Dallas Fort Worth, GMAT Test Prep in Denver, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Quadratic Equations

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #51 : Quadratic Equations

Example Question #52 : Quadratic Equations

Example Question #305 : Equations / Inequalities

Example Question #306 : Equations / Inequalities

Example Question #51 : Quadratic Equations

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: