We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Diameter

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Diameter

The perimeter of a circle is 36 π. What is the diameter of the circle?

Possible Answers:

Correct answer:

Explanation:

The perimeter of a circle = 2 πr = πd

Therefore d = 36

Report an Error

Example Question #2 : How To Find The Length Of The Diameter

Two legs of a right triangle measure 3 and 4, respectively. What is the area of the circle that circumscribes the triangle?

Possible Answers:

$6.25\pi$

$5\pi$

$6\pi$

$12.5\pi$

$25\pi$

Correct answer:

$6.25\pi$

Explanation:

For the circle to contain all 3 vertices, the hypotenuse must be the diameter of the circle. The hypotenuse, and therefore the diameter, is 5, since this must be a 3-4-5 right triangle.

The equation for the area of a circle is A = πr².

$A=\pi (5/2)^2=6.25\pi$

Report an Error

Example Question #1 : Diameter

If a circle has an area of $49\pi$ , what is the diameter of the circle?

Possible Answers:

3.5

Correct answer:

Explanation:

1. Use the area to find the radius:

$Area=\pi r^{2}$

$49\pi=\pi r^{2}$

$49=r^{2}$

r=7

2. Use the radius to find the diameter:

$d=2r=2\cdot 7=14$

Report an Error

Example Question #2 : How To Find The Length Of The Diameter

What is the diameter of a semi-circle that has an area of $25\pi$ ?

Possible Answers:

$5\sqrt{2}$

$10\sqrt{2}$

$25\sqrt{3}$

Correct answer:

$10\sqrt{2}$

Explanation:

To begin, be very careful to note that the question asks about a semi-circle—not a complete circle! This means that a complete circle composed out of two of these semi-circles would have an area of $50\pi$ . Now, from this, we can use our area formula, which is:

$A=\pi r^2$

For our data, this is:

$50\pi=\pi r^2$

Solving for , we get:

$r=\sqrt{50}$

This can be simplified to:

$r = 5\sqrt{2}$

The diameter is , which is $2 * 5\sqrt{2}$ or $10\sqrt{2}$ .

Report an Error

Example Question #4 : How To Find The Length Of The Diameter

A circle has an area of $39\pi$ . What is the diameter of the circle?

Possible Answers:

$2\sqrt{39\pi }$

$\sqrt{39}$

$2\sqrt{39}\pi$

$2\sqrt{39}$

$\sqrt{39\pi }$

Correct answer:

$2\sqrt{39}$

Explanation:

The equation for the area of a circle is $\pi r^2$ , which in this case equals $39\pi$ . Therefore, r^2 = 39. The only thing squared that equals an integer (which is not a perfect root) is that number under a square root. Therefore, $r=\sqrt{39}$ . Since diameter is twice the radius, $d=2\sqrt{39}.$

Report an Error

Example Question #1 : Diameter

Find the diameter given the radius is .

Possible Answers:

$\frac{3}{2}$

Correct answer:

Explanation:

Diameter is simply twice the radius. Therefore, 2*3=6 .

Report an Error

Example Question #2 : Diameter

Find the length of the diameter of a circle given the area is $4\pi$ .

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the area of a circle, solve for r, and multiply by 2 to get the diameter. Thus,

$A=\pi{r^2}\Rightarrow r=\sqrt{\frac{A}{\pi}}$

$r=\sqrt{\frac{4\pi}{\pi}}=\sqrt{4}=2$

d=2r=2*2=4

Report an Error

Example Question #6 : How To Find The Length Of The Diameter

In a group of students, it was decided that a pizza would be divided according to its crust size. Every student wanted 3 inches of crust (measured from the outermost point of the pizza). If the pizza in question had a diameter of 14 inches, what percentage of the pizza was wasted by this manner of cutting the pizza? Round to the nearest hundredth.

Possible Answers:

$66.08\%$

$4.51\%$

$14.66\%$

$5.71\%$

$2.81\%$

Correct answer:

$4.51\%$

Explanation:

What we are looking at is a way of dividing the pizza according to arc lengths of the crust. Thus, we need to know the total circumference first. Since the diameter is , we know that the circumference is $14\pi$ . Now, we want to ask how many ways we can divide up the pizza into pieces of inch crust. This is:

$\frac{14\pi}{3}$ or approximately 14.66... pieces.

What you need to do is take this amount and subtract off . This is the amount of crust that is wasted. You can then merely divide it by the original amount of divisions:

$\frac{0.66076571675237...}{14.66076571675237....}=0.04507034144863....$

(You do not need to work in exact area or length. These relative values work fine.)

This is about $4.51\%$ of the pizza that is wasted.

Report an Error

Example Question #2 : How To Find The Length Of The Diameter

A circle has an area of $\textup{in}^{2}$ . What is its diameter?

Possible Answers:

5.62 $\textup{in}$

2.81 $\textup{in}$

8.14 $\textup{in}$

7.57 $\textup{in}$

3.78 $\textup{in}$

Correct answer:

7.57 $\textup{in}$

Explanation:

To solve a question like this, first remember that the area of a circle is defined as:

$A=\pi r^2$

For your data, this is:

$45 = \pi r^2$

To solve for , first divide both sides by $\pi$ . Then take the square root of both sides. Thus you get:

r =3.78469878303024...

The diameter of the circle is just double that:

d=7.56939756606048

Rounding to the nearest hundredth, you get 7.57 .

Report an Error

Example Question #1 : Diameter And Chords

Let represent the area of a circle and represent its circumference. Which of the following equations expresses in terms of ?

Possible Answers:

C^2

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ , and the formula for circumference is $C=2\pi r$ . If we solve for C in terms of r, we get
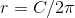
$r=C/2\pi$ .

We can then substitute this value of r into the formula for the area:

$A=\pi r^2$

$=\pi (C/2\pi )^2$

$=C^2\pi /4\pi ^2$

$=C^2/4\pi$

Report an Error

View ACT Math Tutors

MEER
Certified Tutor

IIT , Master's/Graduate, Microelectronics .

View ACT Math Tutors

Margaret
Certified Tutor

View ACT Math Tutors

Sarah
Certified Tutor

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in Miami, SAT Courses & Classes in New York City, MCAT Courses & Classes in Boston, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Denver, Spanish Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Chicago, MCAT Test Prep in Houston, GMAT Test Prep in Miami, LSAT Test Prep in Dallas Fort Worth, ACT Test Prep in New York City, SAT Test Prep in Chicago, ISEE Test Prep in Washington DC, GMAT Test Prep in Seattle, GMAT Test Prep in Boston, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Diameter

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #2 : Diameter

Example Question #2 : How To Find The Length Of The Diameter

Example Question #1 : Diameter

Example Question #2 : How To Find The Length Of The Diameter

Example Question #4 : How To Find The Length Of The Diameter

Example Question #1 : Diameter

Example Question #2 : Diameter

Example Question #6 : How To Find The Length Of The Diameter

Example Question #2 : How To Find The Length Of The Diameter

Example Question #1 : Diameter And Chords

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: