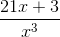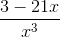Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : How To Multiply Rational Expressions

Give the product in simplified form:

$\frac{x^{3}- 8}{x^{3}+8} \cdot \frac{x+2}{x-2}$

Possible Answers:

$\frac{ x ^{2}-4x+4 }{ x ^{2}+4x+4 }$

$\frac{ x ^{2}+4x+4 }{ x ^{2}-4x+4 }$

$\frac{ x ^{2}-2x+4 }{ x ^{2}+2x+4 }$

$\frac{ x ^{2}+2x+4 }{ x ^{2}-2x+4 }$

Correct answer:

$\frac{ x ^{2}+2x+4 }{ x ^{2}-2x+4 }$

Explanation:

Factor the numerator and denominator in the first fraction, cross-cancel common factors, then multiply out.

$\frac{x^{3}- 8}{x^{3}+8} \cdot \frac{x+2}{x-2}$

$=\frac{\left (x-2 \right )\left (x ^{2}+2x+4 \right )}{ \left (x+2 \right )\left (x ^{2}-2x+4 \right )} \cdot \frac{x+2}{x-2}$

$=\frac{ x ^{2}+2x+4 }{ x ^{2}-2x+4 }$

Report an Error

Example Question #21 : Expressions

Give the product in simplified form:

$\frac{x^{2}- 4x+4}{x^{2}-16} \cdot \frac{ x^{2}+ 8x + 16}{ x^{2}- 4 }$

Possible Answers:

$\frac{x^{2} +2x-8}{ x^{2} -2x-8 }$

$\frac{x^{2} -2x-8}{ x^{2} +2x-8 }$

$\frac{x^{2}+6x+8 }{x^{2} -6x+8}$

$\frac{x^{2} -6x+8}{x^{2}+6x+8 }$

Correct answer:

$\frac{x^{2} +2x-8}{ x^{2} -2x-8 }$

Explanation:

Factor the numerators and denominators, cross-cancel common factors, then multiply out. Both numerators are perfect square trinomials; both denominators are differences of squares.

$\frac{x^{2}- 4x+4}{x^{2}-16} \cdot \frac{ x^{2}+ 8x + 16}{ x^{2}- 4 }$

$=\frac{(x-2)(x-2)}{(x+4)(x-4)} \cdot \frac{(x+4)(x+4)}{ (x+2)(x-2) }$

$=\frac{(x-2) }{ (x-4)} \cdot \frac{(x+4) }{ (x+2) }$

$=\frac{(x-2)(x+4) }{ (x-4)(x+2) }$

$=\frac{x^{2} +2x-8}{ x^{2} -2x-8 }$

Report an Error

Example Question #1 : How To Multiply Rational Expressions

Give the product in simplified form:

$\frac{x^{2}-x}{x+1} \cdot \frac{x^{2}+1}{ x^{2}-2x+1}$

Possible Answers:

$\frac{x^{3}+x}{ x^{2}-1 }$

$\frac{x^{2}+x}{ x -1 }$

$\frac{x^{2} }{ x -1 }$

$\frac{x^{3} }{ x^{2}-1 }$

Correct answer:

$\frac{x^{3}+x}{ x^{2}-1 }$

Explanation:

Factor the numerators and denominators, cross-cancel common factors, then multiply out. Note that the second numerator is prime.

$\frac{x^{2}-x}{x+1} \cdot \frac{x^{2}+1}{ x^{2}-2x+1}$

$=\frac{x(x-1)}{x+1} \cdot \frac{x^{2}+1}{ (x-1)(x-1)}$

$=\frac{x }{x+1} \cdot \frac{x^{2}+1}{ x-1 }$

$= \frac{x^{3}+x}{ x^{2}-1 }$

Report an Error

Example Question #931 : Algebra

Compute the following: $\frac{x+2}{2-x}+\frac{x-2}{2-x}$

Possible Answers:

$\frac{2x}{1-2x}$

$\frac{x}{2-x}$

$\frac{2x}{2-x}$

Correct answer:

$\frac{2x}{2-x}$

Explanation:

Notice that the denominator are the same for both terms. Since they are both the same, the fractions can be added. The denominator will not change in this problem.

$\frac{x+2}{2-x}+\frac{x-2}{2-x} = \frac{x+2+x-2}{2-x} = \frac{2x}{2-x}$

Report an Error

Example Question #11 : Rational Expressions

Simplify the following rational expression: (9x - 2)/(x²) MINUS (6x - 8)/(x²)

Possible Answers:

3x-10

$\frac{15x+6}{x}$

$\frac{12x-6}{x}$

$\frac{3x+6}{x^{2}}$

Correct answer:

$\frac{3x+6}{x^{2}}$

Explanation:

Since both expressions have a common denominator, x², we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.

Report an Error

Example Question #3 : Rational Expressions

Simplify the following rational expression:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

Possible Answers:

$\frac{x-32}{x^{2}}$

$\frac{13x-32}{x^{2}}$

$\frac{13x-4}{x^{2}}$

$\frac{x-4}{x^{2}}$

$\frac{13x-28}{x^{2}}$

Correct answer:

$\frac{13x-32}{x^{2}}$

Explanation:

Since both fractions in the expression have a common denominator of $x^{2}$ , we can combine like terms into a single numerator over the denominator:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

$=\frac{(7x-18)+(6x-14)}{x^{2}}$

$=\frac{13x-32}{x^{2}}$

Report an Error

Example Question #2 : Expressions

Simplify the following expression:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

Possible Answers:

$\frac{21x-3}{x^3}$

$\frac{3-21x}{x^{3}}$

$\frac{x+3}{x^{3}}$

$\frac{3-x}{x^{3}}$

$\frac{21x+3}{x^{3}}$

Correct answer:

$\frac{21x+3}{x^{3}}$

Explanation:

Since both terms in the expression have the common denominator $x^{3}$ , combine the fractions and simplify the numerators:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

$=\frac{(10x-9)+(11x+12)}{x^{3}}$

$=\frac{21x+3}{x^{3}}$

Report an Error

Example Question #4 : Rational Expressions

Simplify the following rational expression:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

Possible Answers:

$\frac{12x+8}{2x^{2}}$

$\frac{8x+4}{2x^{2}}$

$\frac{6x+4}{2x^{2}}$

$\frac{6x+2}{x^{2}}$

$\frac{6x+8}{2x^{2}}$

Correct answer:

$\frac{6x+2}{x^{2}}$

Explanation:

Since both rational terms in the expression have the common denominator $2x^{2}$ , combine the numerators and simplify like terms:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

$=\frac{(5x-5)+(7x+9)}{2x^{2}}$

$=\frac{12x+4}{2x^{2}}$

$=\frac{6x+2}{x^2}$

Report an Error

Example Question #5 : How To Add Rational Expressions With A Common Denominator

Combine the following rational expressions:

$\frac{3x^2-4x+5}{x+1}+\frac{4x^2-5x+9}{x+1}$

Possible Answers:

$\frac{7x^2 -9x+7}{x-1}$

$\frac{7x^2 +x+14}{x+1}$

$\frac{12x^2 +6x+15}{x+1}$

$\frac{-x^2 -9x+14}{x+1}$

$\frac{7x^2 -9x+14}{x+1}$

Correct answer:

$\frac{7x^2 -9x+14}{x+1}$

Explanation:

When working with complex fractions, it is important not to let them intimidate you. They follow the same rules as regular fractions!

$\frac{3x^2-4x+5}{x+1}+\frac{4x^2-5x+9}{x+1}$

In this case, our problem is made easier by the fact that we already have a common denominator. Nothing fancy is required to start. Simply add the numerators:

$\frac{(3x^2-4x+5)+(4x^2-5x+9)}{x+1}$

For our next step, we need to combine like terms. This is easier to see if we group them together.

$\frac{({\color{Blue} 3x^2+4x^2})+({\color{Red} -4x+-5x})+({\color{DarkOrange} 5+9})}{x+1}$

$\frac{({\color{Blue}7x^2})+({\color{Red} -9x})+({\color{DarkOrange} 14})}{x+1}$

Thus, our final answer is:

$\frac{7x^2 -9x+14}{x+1}$

Report an Error

Example Question #1 : How To Evaluate Algebraic Expressions

If x = y – 3, then (y – x)³=

Possible Answers:

–27

–9

Correct answer:

Explanation:

Solve for equation for y – x = 3. Then, plug in 3 into (y – x)³= 27.

Report an Error

View ACT Math Tutors

Alvin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View ACT Math Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View ACT Math Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Phoenix, SSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in San Diego, SSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Boston, GMAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Los Angeles

Popular Test Prep

MCAT Test Prep in Houston, ACT Test Prep in Philadelphia, SSAT Test Prep in Seattle, ACT Test Prep in San Diego, GMAT Test Prep in Phoenix, MCAT Test Prep in Philadelphia, SAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Denver, MCAT Test Prep in Denver, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #4 : How To Multiply Rational Expressions

Example Question #21 : Expressions

Example Question #1 : How To Multiply Rational Expressions

Example Question #931 : Algebra

Example Question #11 : Rational Expressions

Example Question #3 : Rational Expressions

Example Question #2 : Expressions

Example Question #4 : Rational Expressions

Example Question #5 : How To Add Rational Expressions With A Common Denominator

Example Question #1 : How To Evaluate Algebraic Expressions

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: