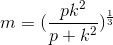To solve this problem you should divide the total number of miles \(\displaystyle \left ( 1\textup{,}642\right )\) by the miles per gallon \(\displaystyle \left ( 32\right )\), and then multiply by the cost of gas per gallon \(\displaystyle \left ( \$3.04\right )\). This gives you \(\displaystyle \$155.99\), which is closest to \(\displaystyle \$156\).

You must plug in \(\displaystyle 6\) for \(\displaystyle \textup{w}\) and \(\displaystyle 4\) for \(\displaystyle \textup{z}\), this means \(\displaystyle 3\textup{w}^{2}-2\textup{z}=\) \(\displaystyle 3\left ( 36\right )-2\left ( 4\right )=100\)   and \(\displaystyle 2\textup{w}^{2}-3\textup{z}=2\left ( 36\right )-3\left ( 4\right )=60\)

\(\displaystyle 100-60=40\) 

The first step is to subtract \(\displaystyle \textup{3t}\) from both sides so you're left with \(\displaystyle 5=4\textup{t}-2\). Next, you add \(\displaystyle 2\) to both sides, giving you \(\displaystyle 7=4\textup{t}\). The final step is to divide by \(\displaystyle 4\), giving you \(\displaystyle \frac{7}{4}=\textup{t}\).

First, set up our two equations. If Karen has seven dollars more than three times as many dollars as Susan, then \(\displaystyle K = 3S +7\). If Karen has half as many dollars as John would if he had two more dollars, then \(\displaystyle K = \frac{J+2}{2}\). The Substitution Property of Equality thus says that \(\displaystyle 3S +7 = \frac{J+2}{2}\). Now, we simply solve for \(\displaystyle S\) in terms of \(\displaystyle J\).

\(\displaystyle 3S +7 = \frac{J+2}{2}\)

\(\displaystyle 6S +14 = J+2\)

\(\displaystyle 6S = J-12\)

\(\displaystyle S = \frac{J-12}{6}\)

If the third day is a Wednesday, then the first day is a Monday. 23 weeks will complete a cycle with the 161st day. Therefore, the fourth day past that, 165, is a Thursday.

We can write an equation for the amount of pizza eaten, with \(\displaystyle x\) as the amount left for Jack.

\(\displaystyle \frac{1}{2} + \frac{1}{3} + x = 1\)

To solve this equation, we must find the lowest common denominator of \(\displaystyle 1/2\) and \(\displaystyle 1/3\). We can list the multiples of \(\displaystyle 2\) and \(\displaystyle 3\) to find the least common multiple:

\(\displaystyle 2: 2, 4, 6, 8, 10, 12, ...\)

\(\displaystyle 3: 3, 6, 12, 15, 18, 21, ...\)

We can see that the least common multiple of \(\displaystyle 2\) and \(\displaystyle 3\) is \(\displaystyle 6\), so we can rewrite each of the fractions with a denominator of \(\displaystyle 6\).

\(\displaystyle \frac{1}{2}\cdot \frac{3}{3} = \frac{3}{6}\)

\(\displaystyle \frac{1}{3}\cdot \frac{2}{2} = \frac{2}{6}\)

When we put these fractions back into the equation, we can solve for \(\displaystyle x\):

\(\displaystyle \frac{3}{6} + \frac{2}{6} + x = 1\)

\(\displaystyle \frac{5}{6} + x = 1\)

\(\displaystyle x = \frac{1}{6}\)

To solve problems where you need to find the slope of a line in a given equation, change the equation so that it matches y-intercept form:

\(\displaystyle y=mx+b\)

For this equation, first move the 3x over to the other side of the equation.

\(\displaystyle 15y + 3x = 4\)

         \(\displaystyle -3x\)   \(\displaystyle -3x\)

The equation should now look like this:

\(\displaystyle 15y = -3x + 4\)

Then, divide by 15 to isolate the variable \(\displaystyle y\).

\(\displaystyle \frac{15y}{15} =-\frac{3x}{15} + \frac{4}{15} \rightarrow y =-\frac{3}{15}x + \frac{4}{15}\)

Then simplify

\(\displaystyle y =-\frac{3}{15}x + \frac{4}{15} \rightarrow y =-\frac{1}{5}x + \frac{4}{15}\)

Whatever number is before the x in the equation (m) is your slope.

\(\displaystyle -\frac{1}{5}\)