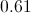We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Rational Numbers

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find A Solution To A Compound Fraction

Convert ${}9\tfrac{2}{5}$ to an improper fraction.

Possible Answers:

${}\frac{47}{5}$

$\frac{78}{5}$

$\frac{23}{5}$

$\frac{90}{5}$

$\frac{16}{5}$

Correct answer:

${}\frac{47}{5}$

Explanation:

To convert into an improper fraction, take the whole number (9) and multiply that with the denominator (5) .

$9\cdot 5=45$

Then, we add that to the numerator which is .

45+2=47

Then we take that sum and put it over th denominator (5) which gives us an answer of:

${}\frac{47}{5}$ .

Report an Error

Example Question #4 : How To Find A Solution To A Compound Fraction

Simplify.

$\frac{\frac{6}{7}}{\frac{8}{3}}\cdot \frac{4}{5}$

Possible Answers:

$\frac{30}{51}$

$\frac{9}{112}$

$\frac{9}{35}$

$\frac{45}{112}$

$\frac{64}{35}$

Correct answer:

$\frac{9}{35}$

Explanation:

Lets focus on the left fraction. Lets try to have three fractions multipled altogether. To acheive this, we can multiply the numerator of the left fraction with the reciprocal of the denominator.

Thus, mutliple the numerator and denominator by $\frac{3}{8}$ .

Now we have $\frac{6}{7}\cdot \frac{3}{8} \cdot \frac{4}{5}$ . We can simplify this by crossing out the to a and the to a .

Then, cross out the into a and the into a . It should look like this:

$\frac{3}{7}\cdot \frac{3}{1}\cdot \frac{1}{5}$ .

Multiply it out and you will get the answer.

$\frac{3}{7}\cdot \frac{3}{1}\cdot \frac{1}{5}=\frac{9}{35}$

Report an Error

Example Question #5 : How To Find A Solution To A Compound Fraction

Solve and simplify.

$\frac{3-\frac{7}{4}}{6-\frac{7}{8}}$

Possible Answers:

$\frac{1}{4}$

$\frac{2}{5}$

$\frac{7}{8}$

$\frac{205}{32}$

$\frac{10}{41}$

Correct answer:

$\frac{10}{41}$

Explanation:

Convert both numerator and denominators into fractions. Convert the integers first to fractions.

$3 \cdot \frac{4}{4}=\frac{12}{4}$

$6 \cdot \frac{8}{8}=\frac{48}{8}$

Now that our numerator and denominator have a common denominator between their fractions we can subtract them.

$\frac{\frac{12}{4}-\frac{7}{4}}{\frac{48}{8}-\frac{7}{8}}=\frac{\frac{5}{4}}{\frac{41}{8}}$

Then multiply top and bottom by $\frac{8}{41}$ as that is the reciprocal of the denominator and when dividing fractions, it is the same as multiplying the numerator by the reciprocal of the denominator.

$\frac{5}{4}\cdot \frac{8}{41}$

Then reduce by crossing out the into a and the into a .

Then multiply to get the answer.

$\frac{5}{1}\cdot \frac{2}{41}=\frac{10}{41}$

Report an Error

Example Question #1 : Compound Fractions

Solve and simplify.

$\frac{1}{2}+\frac{1}{3}\cdot \frac{6}{7}+\frac{1}{5}$

Possible Answers:

$\frac{69}{70}$

$\frac{37}{42}$

$\frac{71}{70}$

$\frac{32}{35}$

$\frac{6}{175}$

Correct answer:

$\frac{69}{70}$

Explanation:

Remember PEMDAS, the order of operations for dealing with expressions which is the acronym that stands for (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction).

Multiplication has priority over addition. Looking at the fractions that are multiplied together we can see the is reduced to and the into a .

The new fraction becomes:

$\frac{1}{2}+\frac{2}{7}+\frac{1}{5}$

Then find least common denominator. In our case it will be 70.

$\frac{1}{2}\cdot \frac{35}{35}+\frac{2}{7}\cdot \frac{10}{10}+\frac{1}{5}\cdot \frac{14}{14}\rightarrow$ $\frac{35}{70}+\frac{20}{70}+\frac{14}{70}$ .

Then add it all up to get the final answer.

$\frac{35}{70}+\frac{20}{70}+\frac{14}{70}=\frac{69}{70}$

Report an Error

Example Question #3 : Compound Fractions

Simplify.

$\frac{14}{4}\left(\frac{3}{7}+\frac{96}{21}\right)-8\left(\frac{17}{8}+\frac{100}{16}\right)$

Possible Answers:

$-\frac{45}{2}$

$\frac{99}{2}$

$\frac{45}{2}$

$-\frac{99}{2}$

$\frac{34}{7}$

Correct answer:

$-\frac{99}{2}$

Explanation:

Remember PEMDAS. Take care of the parentheses first and find least common denominator of the fractions. Next distribute, then add and finally, subtract.

$\frac{14}{4}\left(\frac{9}{21}+\frac{96}{21}\right)-8\left(\frac{34}{16}+\frac{100}{16}\right)$

Working with the parentheses we get:

$\frac{14}{4}\left( \frac{105}{21}\right)-8\left(\frac{134}{16}\right)$

Reduce the to and the to . Then reduce to and to .

$\frac{2}{4}\cdot \frac{105}{3}-\frac{134}{2}$

Multiply first then subtract.

$\frac{210}{12}-\frac{134}{2}$

If I divide the left fraction by , I should be able to match the denominator of the right fraction and also I can subtract easily.

$\frac{35}{2}-\frac{134}{2}=-\frac{99}{2}$

Report an Error

Example Question #3 : Decimals

Express $\frac{8}{15}$ as a decimal.

Possible Answers:

$0.5\overline{3}$

$0.\overline{5}$

0.5

$0.5\overline{8}$

0.52

Correct answer:

$0.5\overline{3}$

Explanation:

Divide 8 by 15:

$\frac{8}{15} = 8 \div 15 = 0.5333...$

The 3 repeats, so the correct choice is $0.5\overline{3}$ .

Report an Error

Example Question #4 : Decimals

Give the decimal equivalent of $\frac{11}{18}$ .

Possible Answers:

0.611

$0.\overline{61}$

$0.6\overline{1}$

0.61

$0.\overline{611}$

Correct answer:

$0.6\overline{1}$

Explanation:

Divide 11 by 18:

$\frac{11}{18} = 11 \div 18 = 0.61111...$

The 1 repeats infinitely, so this can be rewritten as $0.6\overline{1}$ .

Report an Error

Example Question #5 : Decimals

Give the decimal equivalent of $\frac{5}{27}$ .

Possible Answers:

$0.\overline{185}$

0.186

$0.18\overline{5}$

$0.1\overline{85}$

0.185

Correct answer:

$0.\overline{185}$

Explanation:

Divide 5 by 27:

$\frac{5}{27} = 5 \div 27 = 0.185185185...$

The group "185" repeats infinitely, so this can be written as $0.\overline{185}$ .

Report an Error

Example Question #6 : Decimals

Give the decimal equivalent of $\frac{7}{36}$ .

Possible Answers:

$0.\overline{19}$

$0.19\overline{4}$

0.19

0.194

0.195

Correct answer:

$0.19\overline{4}$

Explanation:

Divide 7 by 36:

$\frac{7}{36} = 7 \div 36 = 0.19444444...$

The 4 repeats infinitely, so this can be rewritten as $0.19\overline{4}$ .

Report an Error

Example Question #1 : Decimals With Fractions

Write the value of this expression as a decimal:

$\frac{1}{3} + \frac{1}{4} + \frac{1}{2}$

Possible Answers:

1.25

$0.\overline{923076}$

$1.08\overline{3}$

$0.91\overline{6}$

$0.\overline{3}$

Correct answer:

$1.08\overline{3}$

Explanation:

Simplify the sum by taking the least common denominator, which is 12:

$\frac{1}{3} + \frac{1}{4} + \frac{1}{2}$

$= \frac{1\cdot 4}{3\cdot 4} + \frac{1\cdot 3}{4\cdot 3} + \frac{1\cdot 6}{2\cdot 6}$

$= \frac{ 4}{12} + \frac{3}{12} + \frac{6}{12} = \frac{13}{12}$

Divide 13 by 12:

$\frac{13}{12} = 1. 08333333... = 1.08\overline{3}$

Report an Error

View SSAT- Upper Level Tutors

Kris
Certified Tutor

University of Massachusetts-Dartmouth, Bachelor in Arts, English Composition. University of Massachusetts-Dartmouth, Masters ...

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

View SSAT- Upper Level Tutors

Denisha
Certified Tutor

Nova Southeastern University, Doctor of Medicine, Ayurvedic Medicine. Nova Southeastern University, Master in Public Health, ...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Denver, Physics Tutors in Denver, SAT Tutors in Phoenix, Algebra Tutors in Seattle, Spanish Tutors in Washington DC, GRE Tutors in Philadelphia, ISEE Tutors in Chicago, SSAT Tutors in Seattle, MCAT Tutors in Washington DC, French Tutors in San Francisco-Bay Area

Popular Courses & Classes

SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Houston, ISEE Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Chicago, ACT Courses & Classes in Washington DC, Spanish Courses & Classes in Atlanta, ISEE Courses & Classes in Atlanta, ACT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Houston, SSAT Test Prep in Phoenix, GMAT Test Prep in Chicago, SAT Test Prep in Denver, GMAT Test Prep in Philadelphia, GMAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Chicago, ISEE Test Prep in Miami, ISEE Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Rational Numbers

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #3 : How To Find A Solution To A Compound Fraction

Example Question #4 : How To Find A Solution To A Compound Fraction

Example Question #5 : How To Find A Solution To A Compound Fraction

Example Question #1 : Compound Fractions

Example Question #3 : Compound Fractions

Example Question #3 : Decimals

Example Question #4 : Decimals

Example Question #5 : Decimals

Example Question #6 : Decimals

Example Question #1 : Decimals With Fractions

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: