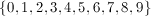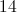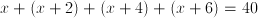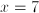The prime digits are 2, 3, 5, and 7.

The perfect square digits are 0, 1, 4, and 9.

The only digits not represent in these two groups are 6 and 8, which are, coincidentally, found in the number 68.

By observing each of these sets, we can easily determine the largest number in each; however, the problem is asking for us to find the greatest possible sum if we select four different integers, one from each set. The largest number is 11. We will either select this number from set Y or set Z.

We will select set

Y for the 11

because the next larger number in set

Z is 10, which is greater than the next largest number is set Y, 7.

We can use set Z for 10.

Because the 10 has already been selected, choosing the integer from W and X should be easy because 9 is the next largest integer from set W

and 

8 is the next largest integer from set X.

11 + 10 + 9 + 8 = 38

If a team's ratio of wins to losses increases from  to  by winning six games, they must have 12 wins initially and 3 losses. 

The rule is as follows: add 2 to the previous number then multiply times 2.

The answer is (16 + 2) * 2 = 36.

In order to find the missing number (X), you must first identify the pattern in the set of numbers. Upon a glance, you can determine that the pattern starts with 4 and then the next number is 2n+1, with n being the preceding number in the set.

For example, let's start with 4. Multiplying 2*4+1 gives us 9, the next number in the set. 

Therefore, the missing number in the set is .

The lower right number of each box is the sum of the other three numbers, which are found as follows:

The upper left numbers are simply the natural numbers in order;

The upper right numbers are the powers of 2, beginning with ;

The lower left numbers are the terms of the Fibonacci sequence, which is formed by setting the first two terms equal to 1 and each subsequent term equal to its predecessors.

Therefore, the ninth box in the sequence includes the number 9 as its upper left entry, and  as its upper right entry. The lower left entry is the ninth Fibonacci number, which can be found as follows:

The lower right entry is the sum of the other entries:

There will be 15 gaps of  long but 16 tick marks because there will be a tick mark on each end of the ruler.

Let x equal the smallest of the four numbers. Therefore:

Therefore the four odd numbers are 7, 9, 11, and 13. Since all are prime except 9, three of the numbers are prime.

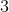
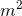
We know that the remainder, , must be less than  by the definition of remainder. Therefore our only choices are , , or . We can test each of these cases. 

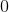
If 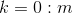  would be divisible by , which we said is not true. 

If : Try . Then . When we divide  by , we have a remainder of . This works! 

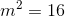
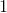
If : Try . Then . When we divide this by , we have a remainder of . Thus, our remainders are not equal. 

Thus, . 

Let's look at a small example, the numbers between 1 and 3 including all endpoints. We have 1, 2, and 3. If we subtract our numbers, we get 2. We need to add one more to get all the desired numbers. We can follow the same process with our larger numbers. 

Take,

 .

Then, adding 1,  

.

Therefore, our answer is