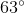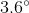Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #23 : Quadrilaterals

If the area of a square is 25 inches squared, what is the perimeter?

Possible Answers:

Not enough information

Correct answer:

Explanation:

The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is $l = \sqrt{25in^{2}}$ or $l=5 in.$ The perimeter of a square is the sum of the length of all 4 sides or $4 \times 5 in. =20 in.$

Report an Error

Example Question #241 : Geometry

Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?

I. Quadrilateral ABCD is a rectangle.

II. Quadrilateral ABCD is a rhombus.

III. Quadrilateral ABCD is a square.

Possible Answers:

II only

II and III only

I and II only

I only

I, II, and III

Correct answer:

I only

Explanation:

Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.

However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.

A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.

The only statement that has to be true is statement I.

The answer is I only.

Report an Error

Example Question #242 : Geometry

If a polygon has 10 sides, what is the measure of each exterior angle?

Possible Answers:

$36^{\circ}$

$3.6^{\circ}$

$72^{\circ}$

$360^{\circ}$

$63^{\circ}$

Correct answer:

$36^{\circ}$

Explanation:

In order to figure this out, we need to remember the formula for finding exterior angles. $\frac{360^{\circ}}{n}$ , where is the number of sides of a polygon. Now we simply do the following calculation.

$\frac{360^{\circ}}{10}=36^{\circ}$

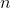
So the measure of each exterior angle is 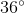$36^{\circ}$ .

Report an Error

Example Question #1 : How To Find The Area Of A Rhombus

A rhombus has a side length of 5. Which of the following is NOT a possible value for its area?

Possible Answers:

Correct answer:

Explanation:

The area of a rhombus will vary as the angles made by its sides change. The "flatter" the rhombus is (with two very small angles and two very large angles, say 2, 178, 2, and 178 degrees), the smaller the area is. There is, of course, a lower bound of zero for the area, but the area can get arbitrarily small. This implies that the correct answer would be the largest choice. In fact, the largest area of a rhombus occurs when all four angles are equal, i.e. when the rhombus is a square. The area of a square of side length 5 is 25, so any value bigger than 25 is impossible to acheive.

Report an Error

Example Question #271 : Plane Geometry

If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.

Possible Answers:

Correct answer:

Explanation:

The area of a rhombus is found by

A = 1/2(d₁)(d₂)

where d₁ and d₂ are the lengths of the diagonals. Substituting for the given values yields

24 = 1/2(d₁)(6)

24 = 3(d₁)

8 = d₁

Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 3² + 4² = 5², each side length is 5, so the perimeter is 5(4) = 20.

Report an Error

Example Question #1 : Circles

Two chords of a circle, $\overline{AB}$ and $\overline{CD}$ , intersect at a point . $\overline{CX}$ is twice as long as $\overline{AX}$ , BX = 20 , and DX = 10 .

Give the length of $\overline{AX}$ .

Possible Answers:

Insufficient information is given to find the length of $\overline{AX}$ .

$10 \sqrt{3}$

$10 \sqrt{2}$

$20\sqrt{2}$

Correct answer:

Insufficient information is given to find the length of $\overline{AX}$ .

Explanation:

Let stand for the length of $\overline{AX}$ ; then the length of $\overline{CX}$ is twice this, or . The figure referenced is below:

Chords

If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,

$AX \cdot BX = CX \cdot DX$

Substituting the appropriate quantities, then solving for :

$t \cdot 20 = 2t \cdot 10$

20 t = 20t

This statement is identically true. Therefore, without further information, we cannot determine the value of - the length of $\overline{AX}$ .

Report an Error

Example Question #1 : Circles

Two chords of a circle, $\overline{AB}$ and $\overline{CD}$ , intersect at a point . $\overline{BX}$ is 12 units longer than $\overline{AX}$ , CX = 8 , and DX = 10 .

Give the length of $\overline{AX}$ (nearest tenth, if applicable)

Possible Answers:

15.0

4.8

3.0

16.8

7.2

Correct answer:

4.8

Explanation:

Let stand for the length of $\overline{AX}$ ; then the length of $\overline{BX}$ is t+12 . The figure referenced is below:

Chords

If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,

$AX \cdot BX = CX \cdot DX$

Substituting the appropriate quantities, then solving for :

$t \cdot (t+12) = 8 \cdot 10$

$t \cdot t+t \cdot 12 = 8 0$

$t ^{2}+12 t = 8 0$

This quadratic equation can be solved by completing the square; since the coefficient of is 12, the square can be completed by adding

$\left (\frac{12}{2} \right ) ^{2} = 6 ^{2} = 36$

to both sides:

$t ^{2}+12 t + 36 = 8 0+ 36$

Restate the trinomial as the square of a binomial:

$(t+6 )^{2 } = 116$

Take the square root of both sides:

$t+6 = \pm \sqrt{116}$

$t+6 \approx - 10.8$ or $t+6 \approx 10.8$

Either

$t+6 \approx - 10.8$ ,

in which case

$t+6 - 6 \approx - 10.8 - 6$

$t \approx -16.8$ ,

$t+6 \approx 10.8$

in which case

$t+6 - 6 \approx 10.8 - 6$

$t \approx 4.8$ ,

Since is a length, we throw out the negative value; it follows that $t \approx 4.8$ , the correct length of $\overline{AX}$ .

Report an Error

Example Question #1 : Chords

A diameter $\overline{AB}$ of a circle is perpendicular to a chord $\overline{CD}$ at a point .

CD= 20, AX= 8

What is the diameter of the circle?

Possible Answers:

$20\frac{1}{2}$

$33\frac{1}{3}$

Insufficient information is given to answer the question.

Correct answer:

$20\frac{1}{2}$

Explanation:

In a circle, a diameter perpendicular to a chord bisects the chord. This makes the midpoint of $\overline{CD}$ ; consequently, $CX =DX = \frac{1}{2} CD = \frac{1}{2} \cdot 20 = 10$ .

The figure referenced is below:

Chords

If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,

$AX \cdot BX = CX \cdot DX$

Setting AX= 8, CX =DX = 10 , and solving for :

$8 \cdot BX = 10 \cdot 10$

$8 \cdot BX = 100$

$8 \cdot BX \div 8 = 100 \div 8$

BX = 12.5

AB = AX + BX = 8 + 12.5 = 20.5 ,

the correct length.

Report an Error

Example Question #1 : Circles

Two chords of a circle, $\overline{AB}$ and $\overline{CD}$ , intersect at a point .

CX = AX + 6

BX = 12

DX = 10

Give the length of $\overline{AX}$ .

Possible Answers:

$3 \sqrt{14}$

$2 \sqrt{30}$

Insufficient information is given to answer the question.

Correct answer:

Explanation:

Let t = AX , in which case CX = t+ 6 ; the figure referenced is below (not drawn to scale).

Chords

If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,

$AX \cdot BX = CX \cdot DX$

Setting AX= t, CX= t+ 6, BX = 12, DX = 10 , and solving for :

$AX \cdot BX = CX \cdot DX$

$t \cdot 12 = (t+6) \cdot 10$

12t = 10t + 60

12t- 10t = 10t + 60 - 10t

2t = 60

$\frac{2t}{2} = \frac{60}{2}$

t = 30 ,

which is the length of $\overline{AX}$ .

Report an Error

Example Question #2 : Circles

A diameter $\overline{AB}$ of a circle is perpendicular to a chord $\overline{CD}$ at point . AX = 12 and BX = 20 . Give the length of $\overline{CD}$ (nearest tenth, if applicable).

Possible Answers:

31.0

16.0

15.5

insufficient information is given to determine the length of $\overline{CD}$ .

32.0

Correct answer:

31.0

Explanation:

A diameter of a circle perpendicular to a chord bisects the chord. Therefore, the point of intersection is the midpoint of $\overline{CD}$ , and

$CX = DX = \frac{1}{2} CD$ .

Let stand for the common length of $\overline{CX}$ and $\overline{DX}$ ,

The figure referenced is below.

Chords

If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords - that is,

$CX \cdot DX = AX \cdot BX$

Set AX = 12 and BX = 20 , and CX = DX = t ; substitute and solve for :

$t \cdot t = 12 \cdot 20$

$t^{2 } = 240$

$t = \sqrt{240} \approx 15.5$

This is the length of $\overline{CX}$ ; the length of $\overline{CD}$ is twice this, so

$CD = 2 \cdot t \approx 2 \cdot 15.5 = 31.0$

Report an Error

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Houston, Spanish Courses & Classes in Miami, ACT Courses & Classes in Houston, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in Philadelphia, MCAT Courses & Classes in New York City, GMAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Houston, GMAT Test Prep in Chicago, MCAT Test Prep in Denver, SSAT Test Prep in Atlanta, ISEE Test Prep in New York City, GMAT Test Prep in Seattle, GRE Test Prep in Los Angeles, SSAT Test Prep in Los Angeles, ACT Test Prep in Denver, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #23 : Quadrilaterals

Example Question #241 : Geometry

Example Question #242 : Geometry

Example Question #1 : How To Find The Area Of A Rhombus

Example Question #271 : Plane Geometry

Example Question #1 : Circles

Example Question #1 : Circles

Example Question #1 : Chords

Example Question #1 : Circles

Example Question #2 : Circles

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: