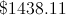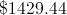To start, we see that Ted works for 20 hours per week for 10 weeks.  This means he works a total of 200 hours over the summer.  He is paid $9 dollars each hour.  Therefore he makes $9 x 200 hours = $1800 total over the summer.  He then has to pay 10% in taxes, or .1 x $1800, leaving him with .  He buys the bike for $500, so he has $1620 - $500 = $1,120 to deposit at the bank.

Now we have to find out how much he will have 5 years later.  Since the bank pays 5% interest each year, we know that he will make 5% of what he has each year.  He starts with $1,120.  5% of this value is .  Adding this to the original $1,120 gives us $1,176.

This is also the same as multiplying instead by 1.05.  We repeat this step 5 times, giving us:

Simple interest is calculated using the following formula:

Where

future value

= present value

= interest rate

For this problem, that means:

Step 1: Set up the system of equations. Simple interest means that interest is calculated at the end of the year. Therefore, the amount of interest at the end of the year is the amount invested times the interest rate.

Let  = the amount put in the investment account

Let  = the amount put in the savings account

Step 2: Use substitution to solve the system.

Substitute  for  in the second equation and solve for :

Step 3: Solve for :

Step 1: We need to convert  percent into a decimal. To do this, we need to move the decimal place back two spots.

. We move the decimal back two spots. The decimal starts right after the .

Step 2: Calculate Simple interest and ending balance for 1 year.

Interest=
Ending Balance=.

Step 3: Calculate Simple interest and ending balance for the next year (2nd year)

Interest=
Ending Balance= 

Step 4: Calculate Simple Interest and ending balance of the third and final year
Interest=
Ending Balance=

Step 5: Add up the interest calculations:

. Over three years, the account gained $158 in interest.

This problem requires knowledge of the compound interest formula, 

Where  is the amount of money owed,  is the sum borrowed,  is the yearly interest rate,  is the amount of times the interest is compounded per year, and  is the number of years.  

We know that the student borrowed $200,000 compounded annually at a 6% interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.

This problem requires knowledge of the compound interest formula, 

Where  is the amount of money owed,  is the sum borrowed,  is the yearly interest rate,  is the amount of times the interest is compounded per year, and  is the number of years.  

We know that the student borrowed $200,000 compounded quarterly at a 6% interest rate, therefore by plugging in those numbers we find what she will owe after she graduates in 4 years.

To reconstruct an original price from a sale price, use:

Original Price – Original Price * Mark-down-percent = Sale Price, or

Original Price * (1 - Mark-down-percent) = Sale Price

To do a double mark-down problem, we must do this twice.  For the 10%:

Original Sale Price * (1 – 10%) = $207.27

Original Sale Price = $207.27/0.9 = $230.30.

For the pre-all-discount price,

Original Price * (1 – 30%) = $230.30

Original Price = $230.30/0.7 = $329.00.

10% of the day one price = 0.1(100) = $10.

Therefore the day two price = 100 - 10 = $90.

10% of the day two price = 0.1(90) = $9.

Therefore the day three price = 90 + 9 = $99.

Let us assume that the original purse is $100. The price after the first reduction is $80. After the second reduction the price is now $56. The difference between 100 and 56 is 44, giving 44% off.

Widget 1 costs $20.

Widget 2 is on sale for 40%($20) off, or $8 off, or $20 – $8 = $12.

Two widgets during the sale cost $20 + $12 = $32.

Two widgets at regular price cost $20 + $20 = $40.

The total amount saved during the sale is $40 – $32 = $8.

This is the savings for two widgets, so the savings for one widget is $8/2 = $4.