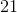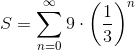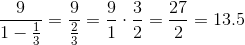Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Sums of Infinite Series

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Sums Of Infinite Series

Find the value for $\sum_{i=0}^{\infty} (\frac{1}{2})^i$

Possible Answers:

1.25

1.5

Correct answer:

Explanation:

To best understand, let's write out the series. So

$\sum_{i=0}^{\infty} (\frac{1}{2})^i = 1+1/2+(1/2)^2 + (1/2)^3+...+(1/2)^\infty$

We can see this is an infinite geometric series with each successive term being multiplied by $\frac{1}{2}$ .

A definition you may wish to remember is

$1+r+r^2+r^3+... +r^\infty= 1/(1-r)$ where stands for the common ratio between the numbers, which in this case is $\frac{1}{2}$ or . So we get

1/(1-r) = 1/(1-.5) = 1/.5 = 2

Report an Error

Example Question #2 : Sums Of Infinite Series

Evaluate:

$1 + \frac{1}{7} + \frac{1}{49} + \frac{1}{343} +...$

Possible Answers:

The series does not converge.

$\frac{7}{6}$

$\frac{4}{3}$

$\frac{6}{5}$

$\frac{9}{8}$

Correct answer:

$\frac{7}{6}$

Explanation:

This is a geometric series whose first term is $a_{0} = 1$ and whose common ratio is $r = \frac{1}{7}$ . The sum of this series is:

$\frac{a_{0}}{1-r} = \frac{1}{1- \frac{1}{7} } = \frac{1}{\frac{7}{7}- \frac{1}{7}}= \frac{1}{\frac{6}{7}} =\frac{7}{6}$

Report an Error

Example Question #3 : Sums Of Infinite Series

Evaluate:

$1 - \frac{1}{6} + \frac{1}{36} - \frac{1}{216} +...$

Possible Answers:

$\frac{6}{7}$

The series does not converge.

$\frac{4}{5}$

$\frac{7}{8}$

$\frac{2}{3}$

Correct answer:

$\frac{6}{7}$

Explanation:

This is a geometric series whose first term is $a_{0} = 1$ and whose common ratio is $r = - \frac{1}{6}$ . The sum of this series is:

$\frac{a_{0}}{1-r} = \frac{1}{1- \left (- \frac{1}{6} \right )} = \frac{1}{\frac{6}{6}+ \frac{1}{6}}= \frac{1}{\frac{7}{6}} =\frac{6}{7}$

Report an Error

Example Question #32 : Sequences And Series

What is the sum of the following infinite series?

$S=2-\frac{1}{3}+1-\frac{1}{9} +\frac{1}{2}-\frac{1}{27}+\frac{1}{4}-\frac{1}{81}+\cdots$

Possible Answers:

$4\tfrac{1}{2}$

$3\tfrac{1}{2}$

$3\tfrac{5}{9}$

diverges

Correct answer:

$3\tfrac{1}{2}$

Explanation:

This series is not alternating - it is the mixture of two geometric series.

The first series has the positive terms.

$2+1+\frac{1}{2}+ \frac{1}{4} + \cdots = 2*\sum\limits_{i=0}^\infty (\frac{1}{2})^i = 2*(\frac{1}{1-\tfrac{1}{2}})=4$

The second series has the negative terms.

$-\frac{1}{3}- \frac{1}{9} -\frac{1}{27}- \cdots = -\frac{1}{3}*\sum\limits_{i=0}^\infty (\frac{1}{3})^i = -\frac{1}{3}*(\frac{1}{1-\tfrac{1}{3}})=-0.5$

The sum of these values is 3.5.

Report an Error

Example Question #1 : Sums Of Infinite Series

What is the sum of the alternating series below?

$10 - 5 + \frac{5}{2} - \frac{5}{4}+\frac{5}{8}-\frac{5}{16}+\cdots$

Possible Answers:

$\frac{10}{3}$

7.5

$\frac{20}{3}$

Correct answer:

$\frac{20}{3}$

Explanation:

The alternating series follows a geometric pattern.

$10 - 5 + \frac{5}{2} - \frac{5}{4} + \cdots = 10*\sum\limits_{i=0}^\infty(-\frac{1}{2})^i$

We can evaluate the geometric series from the formula.

$10*\sum\limits_{i=0}^\infty(-\frac{1}{2})^i = 10*\frac{1}{1+\tfrac{1}{2}} = 10*\frac{2}{3} =\frac{20}{3}$

Report an Error

Example Question #1 : Sums Of Infinite Series

Find the sum of the following infinite series:

$9 + 3 + 1 + \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \frac{1}{81} + \frac{1}{243} + .....$

Possible Answers:

16.5

13.5

20.25

Correct answer:

13.5

Explanation:

Notice that this is an infinite geometric series, with ratio of terms = 1/3. Hence it can be rewritten as:

$S = \sum_{n=0}^{\infty } 9\cdot \bigg(\frac{1}{3}\bigg)^{n}$

Since the ratio, 1/3, has absolute value less than 1, we can find the sum using this formula:

$S = \frac{a_{0}}{1 - r}$

Where a_0 is the first term of the sequence. In this case $a_0 = 9, r = \frac{1}{3}$ , and thus:

$\frac{9}{1-\frac{1}{3}} = \frac{9}{\frac{2}{3}} = \frac{9}{1}\cdot \frac{3}{2}=\frac{27}{2} = 13.5$

Report an Error

Example Question #2 : Sums Of Infinite Series

In the infinite series $a_{1}, a_{2}...a_{n},$ each term $a_{n}=(-2)^{n}$ such that the first two terms are and . What is the sum of the first eight terms in the series?

Possible Answers:

128

-256

-64

210

170

Correct answer:

170

Explanation:

Once you're identified the pattern in the series, you might see a quick way to perform the summation. Since the base of the exponent for each term is negative, the result will be positive if is even, and negative if it is odd. And the series will just list the first 8 powers of 2, with that positive/negative rule attached. So you have:

-2, 4, -8, 16, -32, 64, -128, 256

Note that each "pair" of adjacent numbers has one negative and one positive. for the first pair, -2 + 4 = 2. For the second, -8 + 16 = 8. For the third, -32 + 64 = 32. And so for the fourth, -128 + 256 = 128. You can then quickly sum the values to see that the answer is 170.

Report an Error

View Pre-Calculus Tutors

Yosef
Certified Tutor

Cooper Union for the Advancement of Science and Art, Bachelor of Engineering, Mechanical Engineering. Rensselaer Polytechnic ...

View Pre-Calculus Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

View Pre-Calculus Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in San Diego, LSAT Tutors in Philadelphia, Chemistry Tutors in San Diego, GMAT Tutors in Philadelphia, ACT Tutors in Chicago, MCAT Tutors in New York City, Calculus Tutors in Boston, SSAT Tutors in Boston, Biology Tutors in Houston, Physics Tutors in Boston

Popular Courses & Classes

SAT Courses & Classes in Miami, Spanish Courses & Classes in Philadelphia, SAT Courses & Classes in Seattle, ACT Courses & Classes in Chicago, GMAT Courses & Classes in Houston, GMAT Courses & Classes in Philadelphia, ACT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Houston, SSAT Courses & Classes in Atlanta, LSAT Courses & Classes in New York City

Popular Test Prep

SAT Test Prep in Phoenix, SSAT Test Prep in San Diego, GMAT Test Prep in Denver, SSAT Test Prep in Boston, GMAT Test Prep in Houston, ACT Test Prep in Washington DC, SAT Test Prep in Los Angeles, ACT Test Prep in Chicago, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Sums of Infinite Series

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Sums Of Infinite Series

Example Question #2 : Sums Of Infinite Series

Example Question #3 : Sums Of Infinite Series

Example Question #32 : Sequences And Series

Example Question #1 : Sums Of Infinite Series

Example Question #1 : Sums Of Infinite Series

Example Question #2 : Sums Of Infinite Series

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: