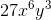Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Polynomials

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Polynomials

Simplify the polynomial.

-2x(2x^2 - 3x + 4) =

Possible Answers:

-4x^3 +6x^2 +8x

-4x^3 -6x^2 - 8x

-4x^3 + 6x^2 - 8x

-4x^2 - 13x

4x^3 - 5x^2 - 8x

Correct answer:

-4x^3 + 6x^2 - 8x

Explanation:

-2x(2x^2-3x + 4) =

(-2x * 2x^2) + (-2x * -3x) + (-2x * 4) =

(-4x^3) + (6x^2) + (-8x) =

-4x^3 + 6x^2 - 8x

Variables without any exponents have an invisable 1 as their exponent.

Report an Error

Example Question #12 : Multiplying And Dividing Polynomials

Simplify: $\frac{b^2-49}{b+7}$

Possible Answers:

-7b

b-7

The expression is already simplified.

b+7

Correct answer:

b-7

Explanation:

In order to simplify this, we need to rewrite the numerator by factorization.

To factor the numerator, we need to look at the factors of the integer value. The factors of the integer value when added together should result in the middle term of the polyinomial. In this particular case there is no middle term therefore, we are looking for a factor that when added together results in a zero term. This is also known as the differences of squares.

$\frac{b^2-49}{b+7} = \frac{(b+7)(b-7)}{b+7}$

Cancel the terms in the numerator and denominator.

The correct answer is: b-7

Report an Error

Example Question #13 : Multiplying And Dividing Polynomials

Simplify: $\frac{x^2-49}{x-7}$

Possible Answers:

7-x

x-7

-7x

x+7

Correct answer:

x+7

Explanation:

In order to divide this polynomial, it is necessary to factor out the numerator.

To factor this polynomial find the two factors of the integer term, , that when added together results in the middle term of the polynomial, .

This particular type of polynomial is known as the difference of perfect squares.

$\frac{x^2-49}{x-7} = \frac{(x+7)(x-7)}{x-7} = x+7$

Report an Error

Example Question #11 : Multiplying And Dividing Polynomials

Multiply: 3x^4(-2x^2+2x-1)

Possible Answers:

-6x^8+6x^4-3x^4

-x^6+5x^5-3x^4

-6x^6+6x^5-3x^4

x^4-x^2-2x-1

-5x^6+5x^5-4x^4

Correct answer:

-6x^6+6x^5-3x^4

Explanation:

Use the distributive property to expand this expression. When powers of similar bases are multiplied, their powers can be added.

3x^4(-2x^2+2x-1) = -6x^6+6x^5-3x^4

Report an Error

Example Question #12 : Multiplying And Dividing Polynomials

Multiply: (3x^2-1)(-8x)

Possible Answers:

-24x^3+8x

-24x^3+8x+1

-24x^3-8x-1

3x^2-8x-1

-24x^2+8x

Correct answer:

-24x^3+8x

Explanation:

Use the distributive property to expand the expression.

(3x^2-1)(-8x) = (3x^2)(-8x)+(-1)(-8x) = -24x^3+8x

Report an Error

Example Question #16 : Multiplying And Dividing Polynomials

Multiply:

(3x^2+4)(2x+8)

Possible Answers:

6x^2+32x+12

6x^3+32x^2+12

6x^3+24x^2+8x+32

6x^3+24x^2+8x+12

30x^2+8x+32

Correct answer:

6x^3+24x^2+8x+32

Explanation:

Use the FOIL method to simplify. FOIL stands for the finding the product of polynomials by multiplying their First, Outer, Inner, and Last terms together.

(3x^2+4)(2x+8) =

Firsts: (3x^2)(2x)

Outers: (3x^2)(8)

Inners: (4)(2x)

Lasts: (4)(8)

Multiply out each term and adding them results in the final polynomial.

Remember when multiplying like bases you add their exponents.

=(3x^2)(2x)+(3x^2)(8)+(4)(2x)+(4)(8)

=6x^3+24x^2+8x+32

Report an Error

Example Question #16 : Multiplying And Dividing Polynomials

Multiply: (2x^2 +2)(3x^2+1)

Possible Answers:

5x^2+6x+1

5x^4+6x^2+2

6x^4+8x^2+2

6x^2+6x+1

6x^4+5x^2+2

Correct answer:

6x^4+8x^2+2

Explanation:

Use the FOIL method to expand the terms.

(2x^2 +2)(3x^2+1) = (2x^2)(3x^2) + (2x^2)(1) + (2)(3x^2)+(2)(1)

Multiply out each term.

$(2x^2)(3x^2) = 2\cdot x\cdot x\cdot 3\cdot x\cdot x = 6x^4$

(2x^2)(1) = 2x^2

$(2)(3x^2) = 2 \cdot 3 \cdot x\cdot x =6x^2$

(2)(1)=2

Combine like-terms and write out the expanded form.

The answer is: 6x^4+8x^2+2

Report an Error

Example Question #58 : Polynomials

Solve the equation below.

$\frac{9x^7}{2x^4}$

Possible Answers:

4.5x^2^8

18x^2^8

18x^1^1

4.5x^3

11x^1^1

Correct answer:

4.5x^3

Explanation:

When dividing with exponents that have different bases, divide the bases then subtract the exponents.

$\frac{9x^7}{2x^4}$

9 / 2 = 4.5

7 - 4 = 3

4.5x^3

Report an Error

Example Question #59 : Polynomials

Multiply the polynomials and simplify.

$(6x^{2})\cdot(4x^{4})=$

Possible Answers:

$10x^{6}$

$24x^{8}$

$10x^{8}$

$24x^{6}$

$24x^{2}$

Correct answer:

$24x^{6}$

Explanation:

To figure out the solution to this problem is to simply multiply the integers normally so

$6\times4=24$

The rule to multiply the same variables with exponents is to add the exponents together. For example,

$x^{2}\times x^{4}= x^{(2+4)}=x^{6}$

So,

$24\times x^{6}=24x^{6}$

Report an Error

Example Question #1 : Power Rule Of Exponents

Simplify:

$\left ( 3x^{2}y \right )^{3}$

Possible Answers:

$27x^{6}y^{3}$

$3x^{2}y^{3}$

$9x^{6}y^{3}$

$9x^{2}y$

$3x^{5}y^{3}$

Correct answer:

$27x^{6}y^{3}$

Explanation:

Recall the Power Rule of Exponents: $\left ( x^{m} \right )^{n}=x^{m*n}$ .

To simplify the expression $\left ( 3x^{2}y \right )^{3}$ , use this rule to distribute the exponents:

$\left ( 3x^{2}y \right )^{3}=3^{3}x^{2*3}y^{3}=27x^{6}y^{3}$

Report an Error

View Pre-Algebra Tutors

Richard
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Chemistry. CUNY Brooklyn College, Master of Arts, Experimental Psychology.

View Pre-Algebra Tutors

Scott
Certified Tutor

Boston University, Bachelor of Science, Film Studies.

View Pre-Algebra Tutors

Cindy
Certified Tutor

Midwestern State University, Masters in Education, Educational Administration.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Atlanta, MCAT Tutors in New York City, ISEE Tutors in Washington DC, Algebra Tutors in San Francisco-Bay Area, Computer Science Tutors in Boston, SAT Tutors in San Francisco-Bay Area, SSAT Tutors in Denver, LSAT Tutors in Seattle, Math Tutors in Philadelphia, Physics Tutors in Miami

Popular Courses & Classes

GMAT Courses & Classes in Chicago, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Denver, SSAT Courses & Classes in Boston, ACT Courses & Classes in Philadelphia, GMAT Courses & Classes in Denver, SSAT Courses & Classes in Atlanta, SAT Courses & Classes in Seattle, ACT Courses & Classes in Houston, SSAT Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in Denver, SAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Houston, GMAT Test Prep in Philadelphia, SSAT Test Prep in Miami, SAT Test Prep in Miami, ACT Test Prep in Philadelphia, GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in San Diego, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Polynomials

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #51 : Polynomials

Example Question #12 : Multiplying And Dividing Polynomials

Example Question #13 : Multiplying And Dividing Polynomials

Example Question #11 : Multiplying And Dividing Polynomials

Example Question #12 : Multiplying And Dividing Polynomials

Example Question #16 : Multiplying And Dividing Polynomials

Example Question #16 : Multiplying And Dividing Polynomials

Example Question #58 : Polynomials

Example Question #59 : Polynomials

Example Question #1 : Power Rule Of Exponents

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: