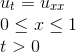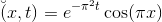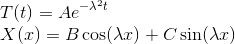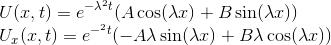We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Partial Differential Equations : Second Order Linear PDEs

Study concepts, example questions & explanations for Partial Differential Equations

Create An Account

All Partial Differential Equations Resources

11 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #10 : Partial Differential Equations

Which of the following describes the physical phenomena that is the wave equation?

Possible Answers:

$\bigtriangledown^2u=f(x,y,z)$

$u_{tt}+c^2\bigtriangledown^4u=0$

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

$u_{xx}+u_{yy}+u_{zz}=0$

Correct answer:

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

Explanation:

When dealing with partial differential equations, there are phenomenons in the physical world that have specific equations related to them in the mathematical world.

Looking at the possible answer selections below, identify the physical phenomena each represents.

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$ is known as the heat equation.

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$ is known as the wave equation.

$u_{xx}+u_{yy}+u_{zz}=0$ is known as the Laplace equation.

$\bigtriangledown^2u=f(x,y,z)$ is known as the Poisson equation.

$u_{tt}+c^2\bigtriangledown^4u=0$ is known as the biharmonic wave equation.

Therefore, the correct answer for the wave equation is

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

Report an Error

Example Question #1 : Heat Equations

Which of the following describes the physical phenomena that is the heat equation?

Possible Answers:

$u_{xx}+u_{yy}+u_{zz}=0$

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

$\bigtriangledown^2u=f(x,y,z)$

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

$u_{tt}+c^2\bigtriangledown^4u=0$

Correct answer:

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

Explanation:

When dealing with partial differential equations, there are phenomenons in the physical world that have specific equations related to them in the mathematical world.

Looking at the possible answer selections below, identify the physical phenomena each represents.

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$ is known as the heat equation.

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$ is known as the wave equation.

$u_{xx}+u_{yy}+u_{zz}=0$ is known as the Laplace equation.

$\bigtriangledown^2u=f(x,y,z)$ is known as the Poisson equation.

$u_{tt}+c^2\bigtriangledown^4u=0$ is known as the biharmonic wave equation.

Therefore, the correct answer for the heat equation is

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

Report an Error

Example Question #1 : Separation Of Variables

Solve for the general solution using separation of variables.

Given the following information:

$\\u_t=u_{xx} \\0\leq x\leq1 \\t>0$

$\\\text{Boundary Conditions: }\left\{\begin{matrix} u_x(0,t)=0\\ u_x(1,t)=0 \end{matrix}\right.$

$\text{Initial Conditions: }u(x,0)=cos(\pi x)$

Possible Answers:

$\u(x,t)=e^{-\pi^2t}\cos(\pi x)+\sin(\pi x)$

$\u(x,t)=e^{-\pi^2t}\sin(\pi x)+\cos(\pi x)$

$\u(x,t)=e^{-\pi^2t}\cos(\pi x)$

$\u(x,t)=e^{-\lambda^2t}\cos(\lambda x)$

$\u(x,t)=e^{-\pi^2t}\sin(\pi x)$

Correct answer:

$\u(x,t)=e^{-\pi^2t}\cos(\pi x)$

Explanation:

Since the question states to use separation of variables the solution looks as follows.

$u(x,0)=cos(\pi x)$

Let

U(x,t)=T(t)X(x)

therefore the partial differential equation becomes

$\\X(x)T'(t)=T(t)X''(x) \\\\\frac{T'(t)}{T(t)}=\frac{X''(x)}{X(x)}=k$

is some constant therefore making the ordinary differential equation,

$\\T'(t)-kT(t)=0 \\X''(x)-kX(x)=0$

In this particular case the constant must be negative.

$\\k=-\lambda^2 \\T'(t)+\lambda^2T(t)=0 \\X''(x)+\lambda^2X(x)=0$

Solving for and results in the following.

$\\T(t)=Ae^{-\lambda^2t} \\X(x)=B\cos(\lambda x)+C\sin(\lambda x)$

From here solve for the general transient solution

$\\U(x,t)=e^{-\lambda ^2t}(A\cos(\lambda x)+B\sin(\lambda x)) \\U_x(x,t)=e^{-\lambs ^2t}(-A\lambda \sin(\lambda x)+B\lambda \cos(\lambda x))$

Lastly apply the boundary conditions to solve for the constants and in turn solve the general solution.

$\\U_x(0,t)=B\lambda e^{-\lambda ^2t}=0 \\B=0 \\u(x,t)=e^{-\pi^2t}\cos(\pi x)$

Report an Error

View Tutors

Ivan
Certified Tutor

Yale University, Bachelor of Science, Economics. Yale University, Bachelor of Science, Mathematics.

View Tutors

Mahal
Certified Tutor

St. Louis University, Bachelor, Computer Science. Pangasinan State University, Master's/Graduate, Special Education.

View Tutors

Jason
Certified Tutor

Brigham Young University, Bachelor, Neuroscience.

All Partial Differential Equations Resources

11 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Miami, Statistics Tutors in Houston, French Tutors in New York City, ISEE Tutors in Atlanta, ISEE Tutors in Washington DC, ACT Tutors in Dallas Fort Worth, Calculus Tutors in Los Angeles, Statistics Tutors in Atlanta, Statistics Tutors in Phoenix, Chemistry Tutors in Denver

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in San Diego, Spanish Courses & Classes in Miami, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Denver, GRE Courses & Classes in New York City, GRE Courses & Classes in Boston, ACT Courses & Classes in Washington DC

Popular Test Prep

ACT Test Prep in Washington DC, SAT Test Prep in Philadelphia, SAT Test Prep in Los Angeles, GRE Test Prep in Denver, ACT Test Prep in San Diego, LSAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Chicago, SSAT Test Prep in Los Angeles, GRE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Partial Differential Equations : Second Order Linear PDEs

Study concepts, example questions & explanations for Partial Differential Equations

All Partial Differential Equations Resources

Example Questions

Example Question #10 : Partial Differential Equations

Example Question #1 : Heat Equations

Example Question #1 : Separation Of Variables

All Partial Differential Equations Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: