ISEE Middle Level Math : Numbers and Operations
Study concepts, example questions & explanations for ISEE Middle Level Math
All ISEE Middle Level Math Resources
Example Questions
Example Question #841 : Numbers And Operations
A sweater that usually costs 
None of these
To find the discounted amount, convert the percent to a decimal and multiply it by the original cost.
Then, subtract the discount amount from the original cost.
Answer:
Example Question #1 : How To Find The Whole From The Part With Percentage
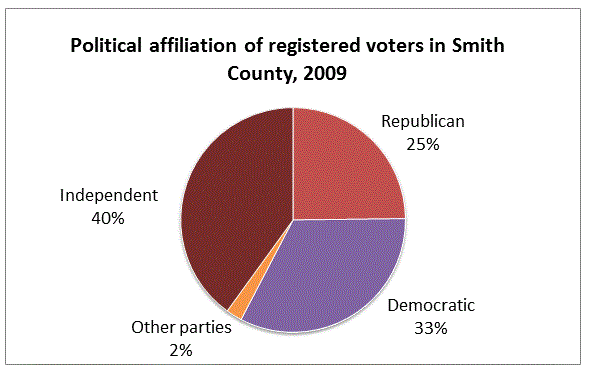
Refer to the above diagram. If there were 15,934 voters who were affiliated with a political party in Smith County in 2009, how many voters (nearest whole number) were there total?
40% of the voters were registered as independents, so 60% were registered as a member of a political party. Since 60% of the voters numbered 15,934, we can find the total number of voters by setting up and solving a proportion:
which rounds to 26,557 voters.
Example Question #82 : Arithmetic
Refer to the above graph. If there were 17,856 registered voters in Smith County in 2009, how many voters were registered as neither Republicans nor Democrats (nearest whole number)?
2% of the voters were registered as members of other parties, and 40% were unaffiliated, so we want to calculate 42% of 17,856, or, equivalently,
which, to the nearest whole number, rounds to 7,500 voters.
Example Question #2 : How To Find The Whole From The Part With Percentage
240 is 30% of what number?
Set up the proportion statement and solve for 
Cross-multiply:
Example Question #6 : Use Proportional Relationships To Solve Multistep Ratio And Percent Problems: Ccss.Math.Content.7.Rp.A.3
420 is 150% of what number?
Set up the proportion statement and solve for 
Example Question #1 : How To Find The Whole From The Part With Percentage
70 is 
Set up the proportion statement and solve for 
Example Question #2 : How To Find The Whole From The Part With Percentage
24 is 25% of what number?
Think 
So:
We have:
Example Question #5 : How To Find The Whole From The Part With Percentage
Julie bought some groceries at the store where she works for $196.57. She got an employee discount of 15%. How much would the same groceries cost a non-employee?
Paying at a 15% discount is equvalent to paying 85% of the original price, so $196.57 is 85% of the original (non-employee) price, or, equivalently, 0.85 times that price. If 
A non-employee would pay $231.26 for the groceries.
Example Question #3 : How To Find The Whole From The Part With Percentage
Becky ate 
This can be solved using a proportion:
Cross multiply and solve for 
Example Question #4 : How To Find The Whole From The Part With Percentage
For her birthday, Susan asks her mother to buy her a car. Susan’s mother agrees to give Susan 150 percent of whatever amount Susan can save up in six months. If Susan saves 
$300
$550
$750
$900
$700
$900
When Susan's mother agreed to match her savings plus fifty percent, she agreed to give Susan 
Before multiplying by the amount Susan saved, we must convert 
Now we multiply 
Susan's mother owes her $
Certified Tutor
Certified Tutor
All ISEE Middle Level Math Resources
