All Introduction to Analysis Resources
Example Questions
Example Question #3 : Intro Analysis
Determine whether the following statement is true or false:
If 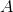



Possible Answers:
True
False
Correct answer:
True
Explanation:
According to the Well-Ordered Principal this statement is true. The following proof illuminate its truth.
Suppose 


Therefore, by the Completeness Axiom the supremum of 
Furthermore, if 


Thus by the Reflection Principal,

exists and

Therefore proving the statement in question true.
Kimone
Certified Tutor
Certified Tutor
Texas Tech University, Bachelor of Science, Mechanical Engineering. Florida State University, Master of Science, Mechanical E...
Francis
Certified Tutor
Certified Tutor
American Public University System, Master of Science, International Relations. The University of Texas at Arlington, Master o...
All Introduction to Analysis Resources
Popular Subjects
GMAT Tutors in Philadelphia, Algebra Tutors in Washington DC, Statistics Tutors in Boston, GMAT Tutors in Phoenix, SAT Tutors in Atlanta, Math Tutors in Los Angeles, Calculus Tutors in New York City, Statistics Tutors in Denver, Algebra Tutors in Los Angeles, ISEE Tutors in Phoenix
Popular Courses & Classes
SSAT Courses & Classes in Atlanta, MCAT Courses & Classes in Atlanta, Spanish Courses & Classes in Chicago, GRE Courses & Classes in San Diego, ISEE Courses & Classes in San Diego, SSAT Courses & Classes in Phoenix, ACT Courses & Classes in San Diego, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Washington DC, LSAT Courses & Classes in Boston
Popular Test Prep
ISEE Test Prep in Atlanta, ISEE Test Prep in San Diego, SAT Test Prep in Denver, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in San Francisco-Bay Area, ACT Test Prep in San Diego, ISEE Test Prep in Seattle, LSAT Test Prep in Houston, MCAT Test Prep in Chicago, ACT Test Prep in New York City




