Intermediate Geometry : How to find the slope of parallel lines
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Slope Of Parallel Lines
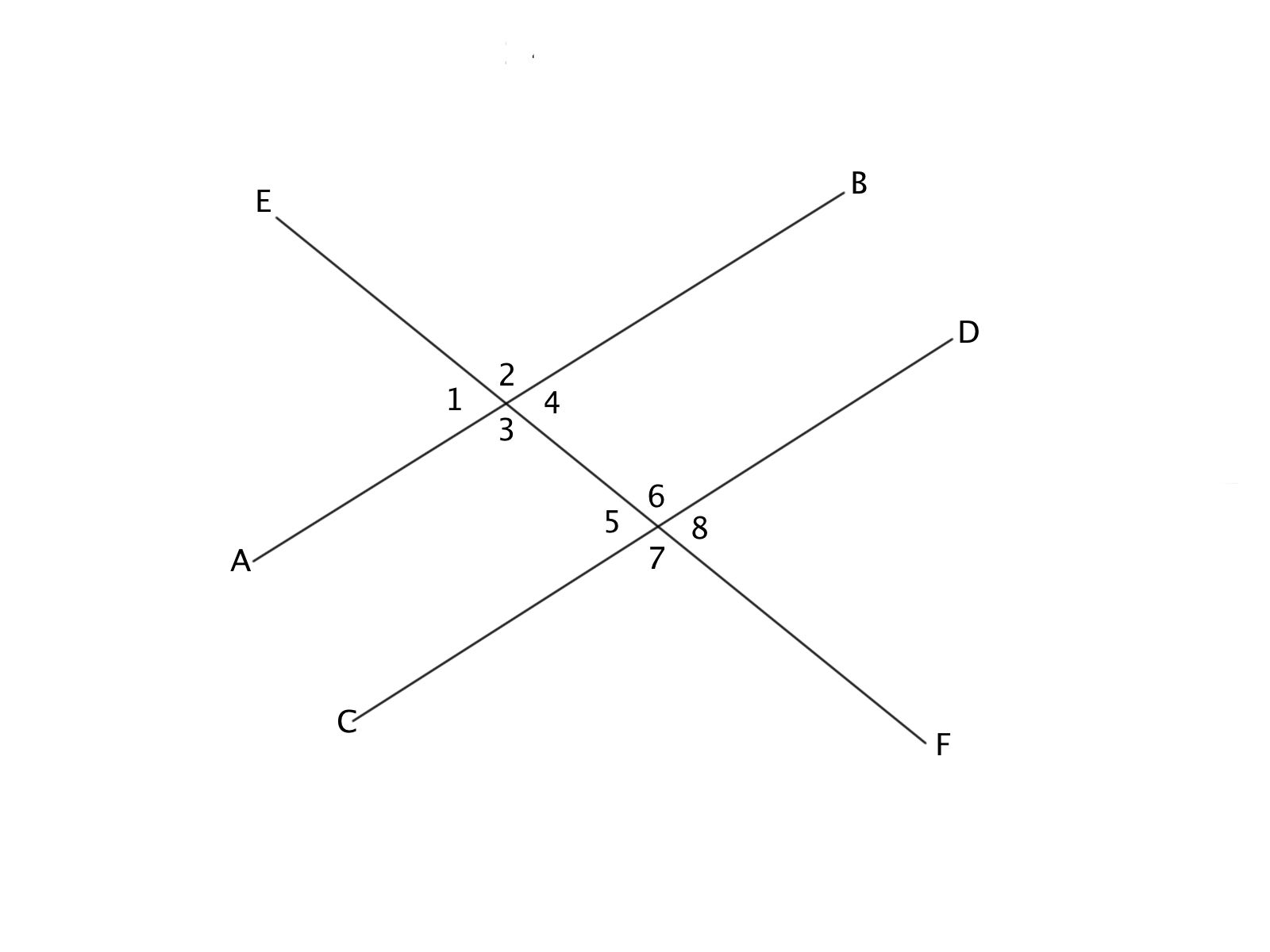
If the slope of line AB is 3x, and Angle 1 and Angle 8 are congruent, what is the slope of line CD, and why?
(1/3)x, because of the Alternate Exterior Angle Theorem
(1/3)x, because of the Vertical Angle Theorem
3x, because of the Alternate Exterior Angle Theorem
3x, because of the Vertical Angle Theorem
3x, because of the Corresponding Angle Theorem
3x, because of the Vertical Angle Theorem
Angles 1 and 8 are a vertical pair. If these angles are congruent, it means that lines AB and CD are parallel based on the Vertical Angle Theorem. Parallel lines have the same slope, so the slope of CD is 3x.
Example Question #2 : How To Find The Slope Of Parallel Lines
The slope of line CD is 4x, and Angle 1 and Angle 5 are congruent. What is the slope of line AB and why?
4x, because of the Vertical Angle Theorem
There is not enough information to determine
4x, because of Corresponding Angles Theorem
4x, because of Alternate Interior Angles Theorem
(1/4)x, because of the Corresponding Angle Theorem
4x, because of Corresponding Angles Theorem
Parallel lines have the same slope. If Angles 1 and 5 are congruent, then lines AB and CD have the same slope (4x) based on the Congruent Angles Theorem.
Example Question #1 : How To Find The Slope Of Parallel Lines
Any line that is parallel to 
Two lines are parallel if and only if they have the same slope. To find the slope, we must put the equation into slope-intercept form, 
Example Question #191 : Coordinate Geometry
Suppose the equation of the first line is 
Rewrite both equations so that they are in slope-intercept form, 
For the first equation:
The slope of the first line is 
Rewrite the second equation in slope-intercept form:
The value of 
Example Question #2 : How To Find The Slope Of Parallel Lines
If the equation of one line is 
Rewrite the equation of the first line in slope-intercept form, 
The value of the slope, 
Example Question #6 : How To Find The Slope Of Parallel Lines
Find a line parallel to the line with the equation:
For two lines to be parallel, they must have the same slope. For a line in 
For the given line, 
Only the following line has the same slope:
Example Question #7 : How To Find The Slope Of Parallel Lines
Find a line parallel to the line with the equation:
For two lines to be parallel, they must have the same slope. For a line in 
For the given line, 
Only the following line has the same slope:
Example Question #8 : How To Find The Slope Of Parallel Lines
Find a line parallel to the line with the equation:
For two lines to be parallel, they must have the same slope. For a line in 
For the given line, 
Only the following line has the same slope:
Example Question #9 : How To Find The Slope Of Parallel Lines
Find a line parallel to the line with the equation:
For two lines to be parallel, they must have the same slope. For a line in 
For the given line, 
Only the following line has the same slope:
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources
