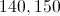We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find an angle in a pentagon

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find An Angle In A Pentagon

The angles at 3 verticies of a pentagon are 60, 80 and 100. Which of the following could NOT be the measures of the other 2 angles?

Possible Answers:

150,150

80,220

140,150

50,250

190,110

Correct answer:

140,150

Explanation:

The sum of the angles in a polygon is

180(n-3)

For a pentagon, this equals 540. Since the first 3 angles add up to 240, the remaining 2 angles must add up to $540-240=300^{\circ}$

Report an Error

Example Question #1 : How To Find An Angle In A Pentagon

What is the sum of three angles in a hexagon if the perimeter of the hexagon is $60\:cm$ ?

Possible Answers:

$240^{\circ}$

$120^{\circ}$

$60^{\circ}$

$360^{\circ}$

$420^{\circ}$

Correct answer:

$360^{\circ}$

Explanation:

The perimeter in this question is irrelevant. Use the interior angle formula to determine the total sum of the angles in a hexagon.

$\Theta =(n-2)\cdot180$

There are six interior angles in a hexagon.

$\Theta =(6-2)\cdot180 = 720^{\circ}$

Each angle will be a sixth of the total angle.

$\frac{720}{6}= 120^{\circ}$

Therefore, the sum of three angles in a hexagon is:

$120^{\circ}+120^{\circ}+120^{\circ}=360^{\circ}$

Report an Error

Example Question #1 : How To Find An Angle In A Pentagon

Add four interior angles in a regular pentagon. What is the result?

Possible Answers:

$576^{\circ}$

$480^{\circ}$

$360^{\circ}$

$432^{\circ}$

$324^{\circ}$

Correct answer:

$432^{\circ}$

Explanation:

Use the interior angle formula to find the total sum of angles in a pentagon.

$\sum \Theta=(n-2) \cdot 180$

n=5 for a pentagon, so substitute this value into the equation and solve:

$\sum \Theta=(5-2) \cdot 180 = 540^{\circ}$

Divide this number by 5, since there are five interior angles.

$\frac{540^{\circ}}{5}=108^{\circ}$

The sum of four interior angles in a regular pentagon is:

$108^{\circ}+108^{\circ}+108^{\circ}+108^{\circ} =432^{\circ}$

Report an Error

Example Question #4 : How To Find An Angle In A Pentagon

What is the sum of two interior angles of a regular pentagon if the perimeter is 6?

Possible Answers:

108

216

130

540

288

Correct answer:

216

Explanation:

The perimeter of a regular pentagon has no effect on the interior angles of the pentagon.

Use the following formula to solve for the sum of all interior angles in the pentagon.

$\sum\theta=(n-2)\cdot 180$

Since there are 5 sides in a pentagon, substitute the side length n=5 .

$\sum\theta=(5-2)\cdot 180=540$

Divide this by 5 to determine the value of each angle, and then multiply by 2 to determine the sum of 2 interior angles.

$\frac{540}{5}=108$

108*2=216

The sum of 2 interior angles of a pentagon is 216 .

Report an Error

Example Question #5 : How To Find An Angle In A Pentagon

Suppose an interior angle of a regular pentagon is 12x . What is ?

Possible Answers:

225

Correct answer:

Explanation:

The pentagon has 5 sides. To find the value of the interior angle of a pentagon, use the following formula to find the sum of all interior angles.

$\sum\theta=(n-2)\cdot 180$

Substitute n=5 .

$\sum\theta=(5-2)\cdot 180=540$

Divide this number by 5 to determine the value of each interior angle.

$\frac{540}{5}=108$

Every interior angle is 108 degrees. The problem states that an interior angle is 12x . Set these two values equal to each other and solve for .

12x=108

x=9

Report an Error

Example Question #1 : How To Find An Angle In A Pentagon

Let the area of a regular pentagon be . What is the value of an interior angle?

Possible Answers:

$216^\circ$

$540^\circ$

$720^\circ$

$108^\circ$

$64^\circ$

Correct answer:

$108^\circ$

Explanation:

Area has no effect on the value of the interior angles of a pentagon. To find the sum of all angles of a pentagon, use the following formula, where is the number of sides:

$\sum\theta=(n-2)\cdot 180$

There are 5 sides in a pentagon.

$\sum\theta=(5-2)\cdot 180=540$

Divide this number by 5 to determine the value of each angle.

$\frac{540}{5}=108^\circ$

Report an Error

Example Question #1 : Pentagons

True or false: Each of the five angles of a regular pentagon measures $120^{\circ }$ .

Possible Answers:

True

False

Correct answer:

False

Explanation:

A regular polygon with sides has congruent angles, each of which measures

$\frac{(N-2)180^{\circ }}{N}$

Setting N = 5 , the common angle measure can be calculated to be

$\frac{(5-2)180^{\circ }}{5} = \frac{3 \cdot 180^{\circ }}{5} = \frac{540^{\circ }}{5} = 108^{\circ }$

The statement is therefore false.

Report an Error

Example Question #8 : How To Find An Angle In A Pentagon

True or false: Each of the exterior angles of a regular pentagon measures $72 ^{\circ }$ .

Possible Answers:

True

False

Correct answer:

True

Explanation:

If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is $360^{\circ }$ . Each exterior angle of a regular pentagon has the same measure, so if we let be that common measure, then

$5t = 360 ^{\circ }$

Solve for :

$5t \div 5 = 360 ^{\circ } \div 5$

$t = 72 ^{\circ }$

The statement is true.

Report an Error

Example Question #9 : How To Find An Angle In A Pentagon

Given: Pentagon PENTA .

$m \angle P = 108 ^{\circ }$

True, false, or undetermined: Pentagon PENTA is regular.

Possible Answers:

False

True

Undetermined

Correct answer:

Undetermined

Explanation:

Suppose Pentagon PENTA is regular. Each angle of a regular polygon of sides has measure

$\frac{(N-2)180^{\circ }}{N}$

A pentagon has 5 sides, so set N = 5 ; each angle of the regular hexagon has measure

$\frac{(5-2)180^{\circ }}{5} = \frac{ 3 \cdot 180^{\circ }}{5} = 108^{\circ }$

Since one angle is given to be of measure $108 ^{\circ }$ , the pentagon might be regular - but without knowing more, it cannot be determined for certain. Therefore, the correct choice is "undetermined".

Report an Error

View Tutors

Matthew
Certified Tutor

Rider University, Bachelor of Science, Chemistry. Rutgers University-Camden, Master of Science, Organic Chemistry.

View Tutors

Bahaeddine
Certified Tutor

Sorbonne University, Bachelor of Science, Mathematics. Sorbonne University, Master of Science, Statistics.

View Tutors

Cassandra
Certified Tutor

Appalachian State University, Bachelor of Science, Chemistry. Appalachian State University, Bachelor of Science, Psychology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Philadelphia, Reading Tutors in Miami, MCAT Tutors in Philadelphia, Calculus Tutors in Atlanta, Spanish Tutors in Washington DC, Biology Tutors in New York City, Calculus Tutors in Miami, Algebra Tutors in Phoenix, Reading Tutors in Atlanta, English Tutors in Phoenix

Popular Courses & Classes

ACT Courses & Classes in Philadelphia, LSAT Courses & Classes in New York City, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Seattle, ACT Courses & Classes in Seattle, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in San Diego, LSAT Courses & Classes in Denver, ISEE Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in San Diego, GMAT Test Prep in Atlanta, LSAT Test Prep in Atlanta, SSAT Test Prep in San Diego, SAT Test Prep in Washington DC, SSAT Test Prep in Miami, GMAT Test Prep in Denver, GRE Test Prep in Philadelphia, ACT Test Prep in Seattle, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find an angle in a pentagon

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find An Angle In A Pentagon

Example Question #1 : How To Find An Angle In A Pentagon

Example Question #1 : How To Find An Angle In A Pentagon

Example Question #4 : How To Find An Angle In A Pentagon

Example Question #5 : How To Find An Angle In A Pentagon

Example Question #1 : How To Find An Angle In A Pentagon

Example Question #1 : Pentagons

Example Question #8 : How To Find An Angle In A Pentagon

Example Question #9 : How To Find An Angle In A Pentagon

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: