All High School Math Resources
Example Questions
Example Question #471 : Plane Geometry
Determine the area of the following equilateral triangle:

The formula for the area of an equilateral triangle is:

where 
Plugging in our value, we get:
Example Question #471 : Geometry
Find the area of an equilateral triangle whose perimeter is
The formula for the perimeter of an equilateral triangle is:
Plugging in our values, we get
The formula for the area of an equilateral triangle is:
Plugging in our values, we get
Example Question #11 : Equilateral Triangles
What is the area of an equilateral triangle with a side length of 5?
Note that an equilateral triangle has equal sides and equal angles. The question gives us the length of the base, 5, but doesn't tell us the height.
If we split the triangle into two equal triangles, each has a base of 5/2 and a hypotenuse of 5.
Therefore we can use the Pythagorean Theorem to solve for the height:
Now we can find the area of the triangle:
Example Question #12 : Equilateral Triangles
An equilateral triangle has a perimeter of 18. What is its area?
Recall that an equilateral triangle also obeys the rules of isosceles triangles. That means that our triangle can be represented as having a height that bisects both the opposite side and the angle from which the height is "dropped." For our triangle, this can be represented as:

Now, although we do not yet know the height, we do know from our 30-60-90 regular triangle that the side opposite the 60° angle is √3 times the length of the side across from the 30° angle. Therefore, we know that the height is 3√3.
Now, the area of a triangle is (1/2)bh. If the height is 3√3 and the base is 6, then the area is (1/2) * 6 * 3√3 = 3 * 3√3 = 9√(3).
Example Question #162 : Geometry
A circle contains 6 copies of a triangle; each joined to the others at the center of the circle, as well as joined to another triangle on the circle’s circumference.
The circumference of the circle is 
What is the area of one of the triangles?
The radius of the circle is 2, from the equation circumference 
To find the height of this triangle, we must divide it down the centerline, which will make two identical 30-60-90 triangles, each with a base of 1 and a hypotenuse of 2. Since these triangles are both right traingles (they have a 90 degree angle in them), we can use the Pythagorean Theorem to solve their height, which will be identical to the height of the equilateral triangle.
We know that the hypotenuse is 2 so 

Now our formula looks like this: 

Let's subtract 1 from each side of that equation, in order to make things a bit simpler:
Now let's apply the square root to each side of the equation, in order to change 

Therefore, the height of our equilateral triangle is
To find the area of our equilateral triangle, we simply have to multiply half the base by the height:
The area of our triangle is
Example Question #201 : Triangles
An equilateral triangle has a side length of 

Not enough information to solve
The altitude, 

In a 






In this scenario:
and
Therefore,

Example Question #202 : Triangles

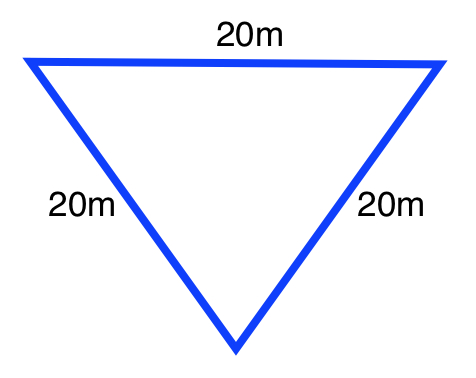
An equilateral triangle has a side length of 

Not enough information to solve
An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value to 



Example Question #1076 : High School Math
What is the height of an equilateral triangle with side 6?
When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the 

Example Question #211 : Triangles
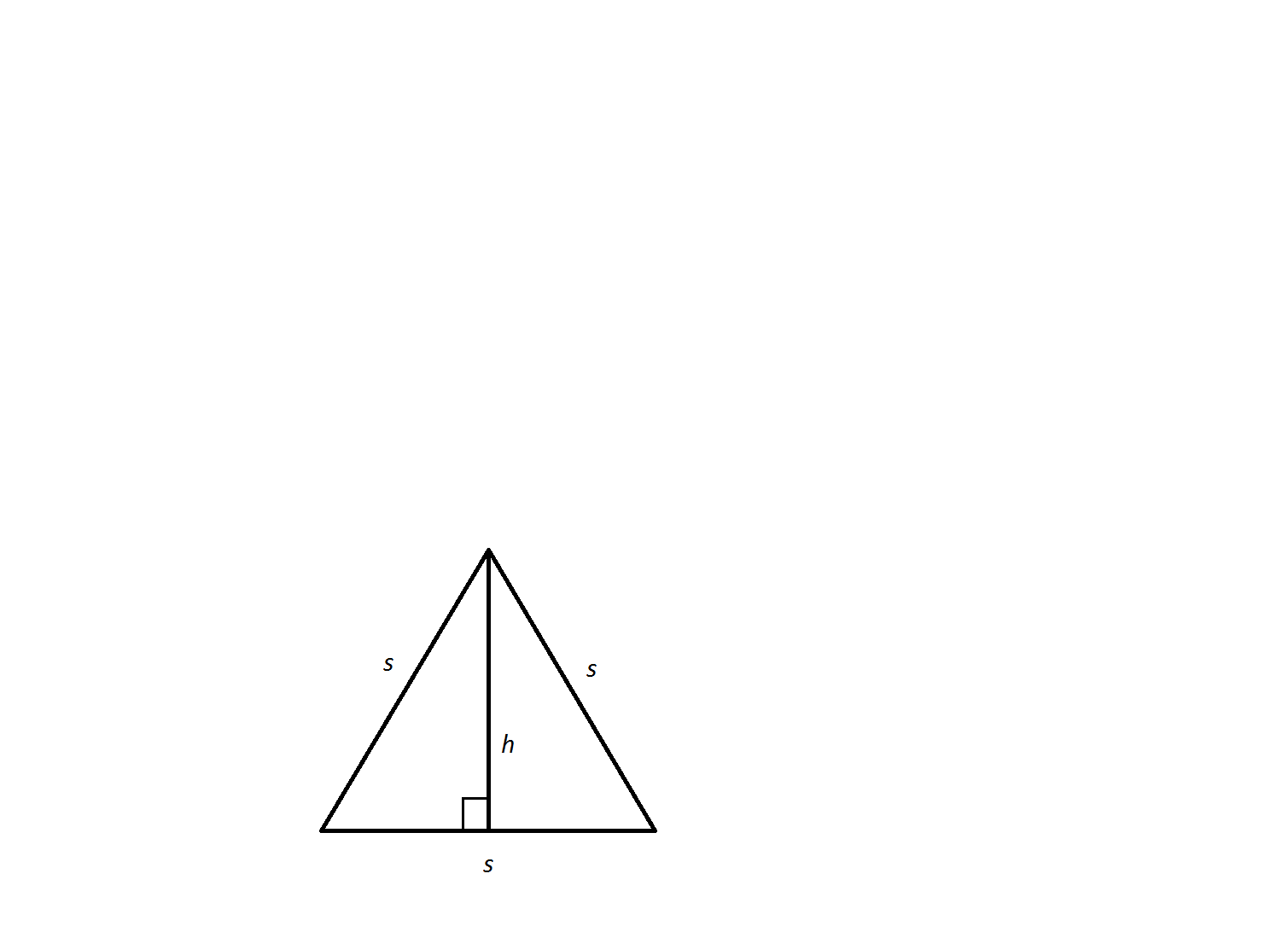
Find the height of the following equilateral triangle:
Each angle in an equilateral triangle is 
Use the formula for 
The formula is:
Where 
If we were to create a 



Example Question #212 : Triangles
Solve for the value of X in the following equilateral triangle:
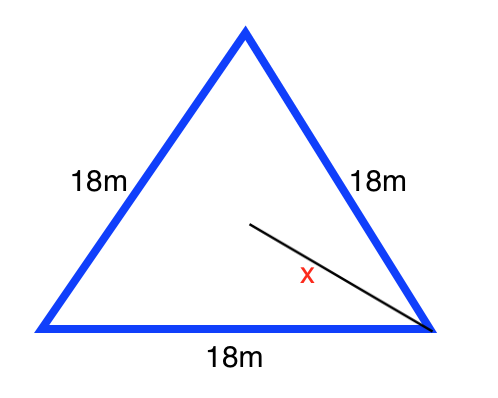
If we draw a line segment between X and the base of the triangle, we form a 
We can use the relationships between the sides of a 
We know the base opposite the 

The value of the height opposite the 


Therefore, the value of X will be twice the value of the height:
All High School Math Resources

















































































