Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the height of an equilateral triangle

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

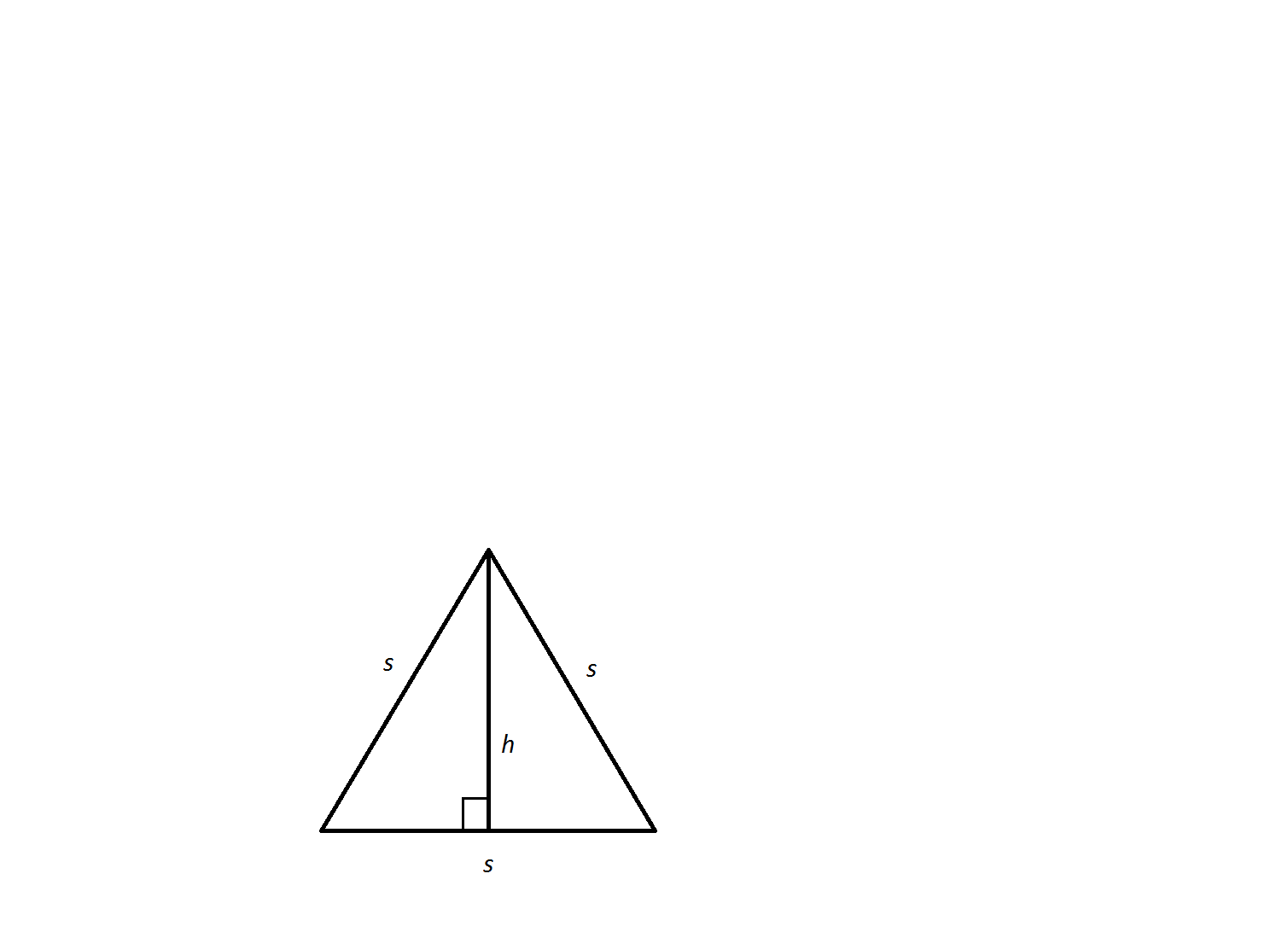
Example Question #1 : How To Find The Height Of An Equilateral Triangle

Equilateral_triangle

An equilateral triangle has a side length of $\sqrt{3}$ . What is the triangle's height $\dpi{100} h$ ?

Possible Answers:

$\sqrt{3}$

$\frac{\sqrt{3}}2{}$

Not enough information to solve

$\frac{3}{2}$

Correct answer:

$\frac{3}{2}$

Explanation:

The altitude, $\dpi{100} h$ , divides the equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ right triangles and divides the bottom side in half.

In a $30^{\circ}-60^{\circ}-90^{\circ}$ right triangle, the sides of the triangle equal , $x\sqrt{3}$ , and . In these equations equals the length of the smallest side, which in our triangle is $\frac{s}{2}$ or $\frac{\sqrt{3}}{2}$ .

In this scenario:

$h=x\sqrt{3}$

and

$x=\frac{\sqrt{3}}2{}$

Therefore,

$h=\frac{\sqrt{3}}{2}*\frac{\sqrt{3}}{1}$

$\rightarrow\frac{3}{2}$

Report an Error

Example Question #2 : How To Find The Height Of An Equilateral Triangle

Equilateral_triangle

An equilateral triangle has a side length of s=4 cm . What is its height, ?

Possible Answers:

5.19cm

1.73cm

3.46cm

Not enough information to solve

4.36cm

Correct answer:

3.46cm

Explanation:

An altitude slices an equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ triangles. These triangles follow a side-length pattern. The smallest of the two legs equals and the hypotenuse equals . By way of the Pythagorean Theorem, the longest leg or $h=x\sqrt{3}$ .

Therefore, we can find the height of the altitude of this triangle by designating a value to . The hypotenuse of one of the $30^{\circ}-60^{\circ}-90^{\circ}$ is also the side of the original equilateral triangle. Therefore, one can say that 2x=s=4cm and x=2cm .

$h=x\sqrt{3}$

$h=2\sqrt{3}cm$

$\rightarrow3.46cm$

Report an Error

Example Question #481 : Plane Geometry

What is the height of an equilateral triangle with side 6?

Possible Answers:

$3\sqrt{3}$

$6\sqrt{2}$

Correct answer:

$3\sqrt{3}$

Explanation:

When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the $60^{\circ}$ ) is $3\sqrt{3}$ .

Report an Error

Example Question #4 : How To Find The Height Of An Equilateral Triangle

Find the height of the following equilateral triangle:

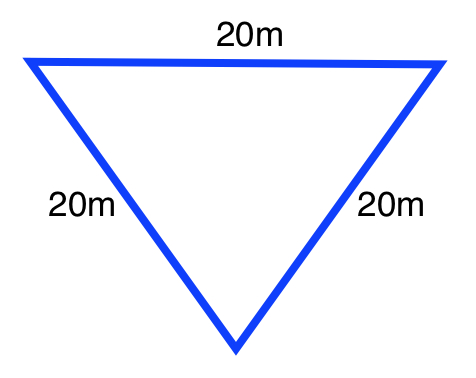
Triangle

Possible Answers:

20m

$15\sqrt{3}m$

$10\sqrt{3}m$

10m

$20\sqrt{3}m$

Correct answer:

$10\sqrt{3}m$

Explanation:

Each angle in an equilateral triangle is $60^{\circ}$ .

Use the formula for 30-60-90 triangles in order to find the length of the height.

The formula is:

$a-a\sqrt{3}-2a$

Where is the length of the side opposite the $\measuredangle 30$

If we were to create a 30-60-90 triangle by drawing the height, the length of the side is 20m , the base is 10m , and the height is $10\sqrt{3}m$ .

Report an Error

Example Question #5 : How To Find The Height Of An Equilateral Triangle

Solve for the value of X in the following equilateral triangle:

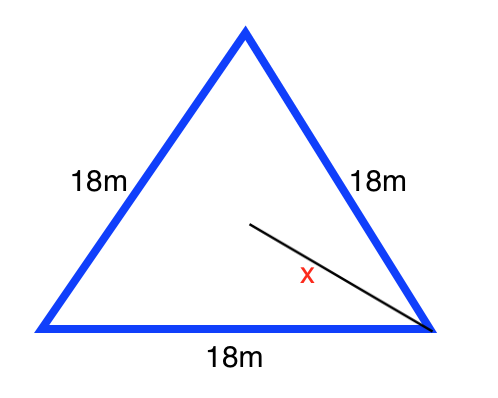
Screen_shot_2014-02-27_at_6.35.43_pm

Possible Answers:

$3\sqrt{3}m$

$6\sqrt{3}m$

$9\sqrt{3}m$

Correct answer:

$6\sqrt{3}m$

Explanation:

If we draw a line segment between X and the base of the triangle, we form a 30-60-90 triangle.

We can use the relationships between the sides of a 30-60-90 triangle in order to find the length of X.

We know the base opposite the $\measuredangle60$ is .

The value of the height opposite the $\measuredangle30$ must then be $\frac{9m\sqrt{3}}{3}$ , or $3\sqrt{3}m$ .

Therefore, the value of X will be twice the value of the height:

$X = 2(3\sqrt{3}m)=6\sqrt{3}m$

Report an Error

Example Question #1 : How To Find The Height Of An Equilateral Triangle

What is the height of an equilateral triangle with a side length of 8 in?

Possible Answers:

$4\sqrt{2}$

$6\sqrt{2}$

$6\sqrt{3}$

$4\sqrt{3}$

Correct answer:

$4\sqrt{3}$

Explanation:

An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.

To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of , $x\sqrt{3}$ , and . The hypoteneuse, the side opposite the 90 degree angle, is the full length of one side of the triangle and is equal to . Using this information, we can find the lengths of each side fo the special triangle.

$8=2x\rightarrow 4=x\rightarrow 4\sqrt{3}=x\sqrt{3}$

The side with length $x\sqrt{3}$ will be the height (opposite the 60 degree angle). The height is $4\sqrt{3}$ inches.

Report an Error

View Tutors

Matt
Certified Tutor

View Tutors

Francisco
Certified Tutor

The University of Texas at El Paso, Bachelor of Science, Physics.

View Tutors

Danielle
Certified Tutor

Florida State University, Bachelors, English. Florida State University, Current Grad Student, History.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Dallas Fort Worth, ISEE Tutors in Philadelphia, MCAT Tutors in Phoenix, Statistics Tutors in Philadelphia, ISEE Tutors in San Francisco-Bay Area, Physics Tutors in Denver, Biology Tutors in Washington DC, Calculus Tutors in Chicago, Calculus Tutors in Washington DC, GMAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

MCAT Courses & Classes in Houston, MCAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Diego, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Chicago, GRE Courses & Classes in Miami, Spanish Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Atlanta, SAT Test Prep in Denver, SAT Test Prep in Seattle, SAT Test Prep in Los Angeles, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Chicago, LSAT Test Prep in Atlanta, ISEE Test Prep in Philadelphia, SSAT Test Prep in Boston, GMAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the height of an equilateral triangle

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Height Of An Equilateral Triangle

Example Question #2 : How To Find The Height Of An Equilateral Triangle

Example Question #481 : Plane Geometry

Example Question #4 : How To Find The Height Of An Equilateral Triangle

Example Question #5 : How To Find The Height Of An Equilateral Triangle

Example Question #1 : How To Find The Height Of An Equilateral Triangle

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: