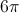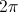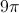We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find The Area Of A Triangle In Pre Algebra

What is the area of a triangle with a base of and a height of ?

Possible Answers:

Correct answer:

Explanation:

To find the area of a triangle, use the equation:

$Area=\frac{1}{2}(Base)(Height)$

Substitute the given values for base and height into the equation:

$Area=\frac{1}{2}(5)(14)$

Area=35

Report an Error

Example Question #731 : High School Math

Find the area of a triangle with a base of 3 inches and a height of 14 inches.

Possible Answers:

$48\ in^{2}$

$21\ in^{2}$

$52\ in^{2}$

$42\ in^{2}$

$24\ in^{2}$

Correct answer:

$21\ in^{2}$

Explanation:

Apply the formula for the area of a triangle: $\frac{1}{2}bh$

A = 3 * 14 * (1/2) = 21

Make sure that your units are squared.

Report an Error

Example Question #732 : High School Math

Find the area of a triangle with a base of 16 meters and a height of 4 meters.

Possible Answers:

$112\ m^{2}$

$108\ m^{2}$

$32\ m^{2}$

$64\ m^{2}$

$30\ m^{2}$

Correct answer:

$32\ m^{2}$

Explanation:

Area of a triangle = $\frac{1}{2}bh$

= (1/2) * 16 * 4

= 32

Report an Error

Example Question #733 : High School Math

What is the area of this triangle?

Possible Answers:

Correct answer:

Explanation:

The area of a triangle can be calculated using this equation $\small A=\frac{1}{2}bh$ .

In this question, the base, , is . The height, , is .

$\small A=\frac{1}{2}bh=\frac{1}{2}(8)(6)=\frac{1}{2}(48)=24$

Report an Error

Example Question #1 : How To Find The Area Of A Circle In Pre Algebra

What is the area of circle with a radius of ?

Possible Answers:

$18\pi$

$9\pi$

$81\pi$

Correct answer:

$81\pi$

Explanation:

To find the area of a circle you must plug the radius into in the following equation

In this case the radius is so we plug it into to get $9^{2}=81$

We then multiply it by $\pi$ to get our answer $A=81\pi$ .

Report an Error

Example Question #1 : How To Find The Area Of A Circle In Pre Algebra

What is the area of a circle with radius of ?

Possible Answers:

$9\pi$

$2\pi$

$3\pi$

$27\pi$

$6\pi$

Correct answer:

$9\pi$

Explanation:

The formula for the area of a circle is $A=\pi r^2$ .

Plug in our given values:

$A=\pi r^2$

$A=\pi*3^2$

$A=9\pi$

Report an Error

Example Question #2 : How To Find The Area Of A Circle In Pre Algebra

What is the area of a circle with a radius of ?

Possible Answers:

$2\pi$

$16\pi$

$32\pi$

$4\pi$

$8\pi$

Correct answer:

$16\pi$

Explanation:

The formula for the area of a circle is $A=\pi r^2$ .

Plug in the information given and solve:

$A=\pi * 4^2$

Remember, a number squared is just the same as that number times itself:

$A=\pi*(4*4)$

$A=16\pi$

Report an Error

Example Question #4 : How To Find The Area Of A Circle In Pre Algebra

If the area of a circle is $64\pi$ , what is the radius of the circle?

Possible Answers:

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ .

Plug in the information given and solve:

$64\pi = \pi r^2$

Notice that the $\pi$ 's cancel out:

64=r^2

Take the square root of both sides:

$\sqrt{64}=\sqrt{r^2}$

8=r

Report an Error

Example Question #57 : Area Of A Figure

If the diameter of a circle is , what is the area of that circle?

Possible Answers:

$484\pi$

$121\pi$

$11\pi$

$22\pi$

$66\pi$

Correct answer:

$121\pi$

Explanation:

The area of a circle is $A=\pi r^2$ , but the problem gives us the diameter and not the radius.

The diameter is twice the radius, so d=2r . We can plug in our given values to find the radius:

22=2r

$\frac{22}{2}=r$

11=r

Now we can plug this value into our equation for area:

$A=\pi r^2$

$A=\pi*11^2$

$A=\pi *121$

$A=121\pi$

Report an Error

Example Question #58 : Area Of A Figure

If the area of a circle is $36\pi$ , what is the length of the radius?

Possible Answers:

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ . Plug in our given information to solve:

$A=\pi r^2$

$36\pi=\pi r^2$

The $\pi$ 's cancel out, leaving us with:

36=r^2

Take the square root of both sides:

$\sqrt{36}=\sqrt{r^2}$

6=r

Report an Error

View Tutors

Manasa
Certified Tutor

Ramaiah Institute of Technology, Bachelor of Engineering, Telecommunications Engineering.

View Tutors

Hera
Certified Tutor

Benedictine College, Bachelor of Science, Biology Teacher Education. University of Illinois at Chicago, Master of Science, Bi...

View Tutors

Laura
Certified Tutor

New York University, Bachelor in Arts, French.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Dallas Fort Worth, ISEE Tutors in Atlanta, Calculus Tutors in Chicago, SSAT Tutors in San Diego, French Tutors in Dallas Fort Worth, LSAT Tutors in Dallas Fort Worth, GMAT Tutors in Boston, Math Tutors in Los Angeles, English Tutors in Philadelphia, GRE Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Phoenix, MCAT Courses & Classes in Phoenix, SSAT Courses & Classes in Chicago, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Washington DC, LSAT Courses & Classes in Seattle, GMAT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in Washington DC, SSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in San Diego, ISEE Test Prep in Philadelphia, GRE Test Prep in Atlanta, LSAT Test Prep in Atlanta, LSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Phoenix, SAT Test Prep in Chicago, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #11 : How To Find The Area Of A Triangle In Pre Algebra

Example Question #731 : High School Math

Example Question #732 : High School Math

Example Question #733 : High School Math

Example Question #1 : How To Find The Area Of A Circle In Pre Algebra

Example Question #1 : How To Find The Area Of A Circle In Pre Algebra

Example Question #2 : How To Find The Area Of A Circle In Pre Algebra

Example Question #4 : How To Find The Area Of A Circle In Pre Algebra

Example Question #57 : Area Of A Figure

Example Question #58 : Area Of A Figure

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: