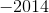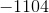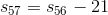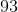GRE Math : Arithmetic Sequences

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

The sequence s_n $\displaystyle s_n$ is defined by:

$\displaystyle s_n=s_n_-_1 -21$

s_1=93 $\displaystyle s_1=93$

What is the value of s_5_7 $\displaystyle s_5_7$?

Possible Answers:

$\displaystyle -1104$

$\displaystyle -1083$

$\displaystyle -1176$

$\displaystyle -3914$

$\displaystyle -2014$

Correct answer:

$\displaystyle -1083$

Explanation:

For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:

$\displaystyle s_n=s_n_-_1 -21$

This means that for every element in the list, each one is $\displaystyle 21$ less than the one preceding it. For instance:

$\displaystyle s_5_7=s_5_6-21$

Now, notice that the first element is:

$\displaystyle 93$

The second is:

93-21 $\displaystyle 93-21$

The third could be represented as:

$\displaystyle 93-21-21$

And so forth...

Now, notice that for the third element, there are only two instances of $\displaystyle -21$. We could rewrite our sequence:

93-2*21 $\displaystyle 93-2*21$

This value will always "lag behind" by one. Therefore, for the $\displaystyle 57$th element, you will have:

$93-56\cdot21=-1083$ $\displaystyle 93-56\cdot21=-1083$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Los Angeles, GMAT Tutors in New York City, LSAT Tutors in Philadelphia, Chemistry Tutors in Washington DC, English Tutors in Philadelphia, Calculus Tutors in Seattle, SAT Tutors in Washington DC, Math Tutors in New York City, Computer Science Tutors in Phoenix, GMAT Tutors in Boston

Popular Courses & Classes

SAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Denver, MCAT Courses & Classes in Miami, GMAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Houston, GRE Courses & Classes in Miami, GRE Courses & Classes in Boston, ISEE Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in Los Angeles, GMAT Test Prep in Philadelphia, SSAT Test Prep in Miami, LSAT Test Prep in Washington DC, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC, MCAT Test Prep in San Diego, LSAT Test Prep in New York City, LSAT Test Prep in Miami, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Arithmetic Sequences

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details