All GRE Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Square
A square with width of 
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
Therefore the radius must be
Now let's find the area inside the circle using the radius.

Example Question #2 : How To Find The Length Of The Diagonal Of A Square
Quantity A:
The diagonal of a square with a side-length of 
Quantity B:
The side-length of a square with a diagonal of 
The relationship between the two quantities cannot be determined from the information given.
Quantity A is greater.
Both quantities are equal.
Quantity B is greater.
Both quantities are equal.
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of 
In Quantity A, the side-length is 7. Following the proportion:
The diagonal equals 
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:
To find x in this ratio, just isolate x in the hypotenuse:
Divide by
Now, how does Quantity A and Quantity B match up?
On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that 
Divide both sides by
Therefore, both quantities are equal.
Example Question #181 : Plane Geometry
Quantity A:
The side-length of a square with a perimeter of 
Quantity B:
The side-length of a square with an area of 
The relationship cannot be determined from the information given
Both quantities are equal
Quantity A is greater
Quantity B is greater
Quantity A is greater
The first step to a quantitative comparison is to determine whether it can be solved at all with the given knowledge. Since all you need to find the side-length of a square is the perimeter, the area, OR the diagonal and we have one of each for these two quantities, this relationship can be determined. Thus, "the relationship cannot be determined" is out.
Now, to solve both quantities. Quantity A can be solved by translating the perimeter into side lengths: the formula for the perimeter of a square is 

Thus, quantity A is 
Quantity B can be solved by translating the area into side lengths: the formula for the area of a square is 


Thus, quantity B is roughly 
Therefore quantity A is greater.
Example Question #182 : Plane Geometry

Circle 

If the area of Circle 


If the area of Circle 



Simplifying, we get:
We know that 





Notice that the diameter is the same length as a side of the square. Thus, 

Example Question #183 : Plane Geometry

Circle 

The line segment marked with length 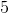

What is the length of side 
This cannot be computed from the given data
You can further fill in your diagram as follows:

Now, we know that the triangle 




For our data, that means:
Simplifying, we know:
Now, make both sides reciprocals:
Finally, solve:
Recall, this is both the length of the side and the diameter of the circle. Hence, you have your answer.
All GRE Math Resources



















































