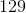GRE Math : How to find the nth term of an arithmetic sequence

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Sequences

The first term in a sequence of integers is 2 and the second term is 10. All subsequent terms are the arithmetic mean of all of the preceding terms. What is the 39th term?

Possible Answers:

600

300

1200

Correct answer:

Explanation:

The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.

Report an Error

Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence

Consider the following sequence of integers:

5, 11, 23, 47

What is the 6^th element in this sequence?

Possible Answers:

189

None of the other answers

191

Correct answer:

191

Explanation:

First, consider the change in each element. Notice that in each case, a given element is twice the preceding one plus one:

11 = 2 * 5 + 1

23 = 11 * 2 + 1

47 = 23 * 2 + 1

To find the 6^th element, continue following this:

The 5^th: 47 * 2 + 1 = 95

The 6^th: 95 * 2 + 1 = 191

Report an Error

Example Question #1 : Sequences

The sequence $\small a_{1}+a_{2}+... +a_{n}$ begins with the numbers 3, 11, 18, . . . and has the $\small n^{th}$ term defined as a_1+2n+n^2 , for $\small n\geq 2$ .

What is the value of the $20^{th}$ term of the sequence?

Possible Answers:

155

163

220

460

443

Correct answer:

443

Explanation:

The first term of the sequence is $\small a_{1}$ , so here $\small a_{1} = 3$ , and we're interested in finding the 20th term, so we'll use n = 20.

Plugging these values into the given expression for the nth term gives us our answer.

a_1+2n+n^2

$\small a_{1} = 3$ and n=20

$\small 3 + 2(20) + 20^{2} = 443$

Report an Error

Example Question #1 : Sequences

In a sequence of numbers, the first two values are 1 and 2. Each successive integer is calculated by adding the previous two and mutliplying that result by 3. What is fifth value in this sequence?

Possible Answers:

126

129

None of the other answers

Correct answer:

126

Explanation:

Our sequence begins as 1, 2.

Element 3: (Element 1 + Element 2) * 3 = (1 + 2) * 3 = 3 * 3 = 9

Element 4: (Element 2 + Element 3) * 3 = (2 + 9) * 3 = 11 * 3 = 33

Element 5: (Element 3 + Element 4) * 3 = (9 + 33) * 3 = 42 * 3 = 126

Report an Error

Example Question #1 : Nth Term Of An Arithmetic Sequence

Let Z represent a sequence of numbers (z_1,z_2,z_3,z_4,...,z_n) wherein each term is defined as seven less than three times the preceding term. If z_3+z_5=142 , what is the first term in the sequence?

Possible Answers:

125

Correct answer:

Explanation:

Let us first write the value of a consecutive term in a numerical format:

$z_{n+1} = 3z_n-7$

Consequently,

$z_n=\frac{z_{n+1}+7}{3}$

Using the first equation, we can define z_5 in terms of z_3 :

z_5=3z_4-7=3(3z_3-7)-7=9z_3-21-7=9z_3-28

This allows us to rewrite

z_3+z_5=142

z_3+9z_3-28=142

Rearrangement of terms allows us to solve for z_3 :

10z_3=170

z_3=17

Now, using our second equation, we can find z_1 , the first term:

$z_{1}=\frac{z_2+7}{3}=\frac{\frac{z_{3}+7}{3}+7}{3}=\frac{\frac{24}{3}+7}{3}=\frac{15}{3}=5$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Philadelphia, ISEE Tutors in Miami, Reading Tutors in San Diego, Chemistry Tutors in Los Angeles, GRE Tutors in San Diego, SAT Tutors in Miami, GMAT Tutors in Washington DC, ISEE Tutors in San Diego, Spanish Tutors in Dallas Fort Worth, Computer Science Tutors in Los Angeles

Popular Courses & Classes

MCAT Courses & Classes in Atlanta, SAT Courses & Classes in Los Angeles, ISEE Courses & Classes in San Diego, SSAT Courses & Classes in Houston, GRE Courses & Classes in San Diego, GMAT Courses & Classes in Houston, ACT Courses & Classes in Denver, ISEE Courses & Classes in Denver, Spanish Courses & Classes in Los Angeles, LSAT Courses & Classes in Chicago

Popular Test Prep

ISEE Test Prep in Houston, ACT Test Prep in Denver, GMAT Test Prep in Dallas Fort Worth, SAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, SAT Test Prep in Chicago, GMAT Test Prep in Miami, LSAT Test Prep in Chicago, ISEE Test Prep in Boston, MCAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : How to find the nth term of an arithmetic sequence

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Sequences

Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence

Example Question #1 : Sequences

Example Question #1 : Sequences

Example Question #1 : Nth Term Of An Arithmetic Sequence

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details