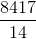GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #14 : How To Evaluate A Fraction

Simplify:

$\frac{\frac{1}{4}+\frac{5}{7}}{\frac{2}{5}}$

Possible Answers:

$\frac{47}{5}$

$\frac{27}{70}$

$\frac{135}{56}$

$\frac{81}{7}$

$\frac{98}{71}$

Correct answer:

$\frac{135}{56}$

Explanation:

Begin by simplifying the numerator.

$\frac{1}{4}+\frac{5}{7}$ has a common denominator of . Therefore, we can rewrite it as:

$\frac{7}{28}+\frac{20}{28}=\frac{27}{28}$

Now, in our original problem this is really is:

$\frac{\frac{27}{28}}{\frac{2}{5}}$

When you divide by a fraction, you really multiply by the reciprocal:

$\frac{\frac{27}{28}}{\frac{2}{5}}=\frac{27}{28} \cdot\frac{5}{2}=\frac{135}{56}$

Report an Error

Example Question #41 : Algebraic Fractions

Simplify:

$\frac{\frac{81}{5}+\frac{7}{25}}{\frac{1}{9}-\frac{2}{7}}$

Possible Answers:

$-\frac{551}{12}$

$\frac{8414}{41}$

$-\frac{4532}{1575}$

$\frac{8417}{14}$

$-\frac{25956}{275}$

Correct answer:

$-\frac{25956}{275}$

Explanation:

Begin by simplifying the numerator and the denominator.

Numerator

$\frac{81}{5}+\frac{7}{25}$ has a common denominator of . Therefore, we have:

$\frac{405}{25}+\frac{7}{25} = \frac{412}{25}$

Denominator

$\frac{1}{9}-\frac{2}{7}$ has a common denominator of . Therefore, we have:

$\frac{7}{63}-\frac{18}{63}=-\frac{11}{63}$

Now, reconstructing our fraction, we have:

$\frac{\frac{412}{25}}{-\frac{11}{63}}$

To make this division work, you multiply the numerator by the reciprocal of the denominator:

$\frac{\frac{412}{25}}{-\frac{11}{63}} = \frac{412}{25} \cdot -\frac{63}{11} =-\frac{25956}{275}$

Report an Error

Example Question #13 : How To Evaluate A Fraction

Simplify: $(\frac{x-4}{0.5})\div (\frac{1}{x+4})$

Possible Answers:

2x^2-32

$\frac{1}{2}$

None of the other answer choices are correct.

$\frac{3}{2x^2}-16$

Correct answer:

2x^2-32

Explanation:

Recall that dividing is equivalent multiplying by the reciprocal. Therefore, ((x - 4) / (1 / 2)) / (1 / (x + 4)) = ((x - 4) * 2) * (x + 4) / 1.

Let's simplify this further:

(2x – 8) * (x + 4) = 2x² – 8x + 8x – 32 = 2x² – 32

Report an Error

Example Question #14 : How To Evaluate A Fraction

Solve for :

$\frac{3x}{8}+12=\frac{1}{3}-2x$

Possible Answers:

$-\frac{81}{13}$

$-\frac{280}{57}$

$-\frac{5}{7}$

$\frac{100}{21}$

$\frac{43}{2}$

Correct answer:

$-\frac{280}{57}$

Explanation:

Begin by isolating the variables:

$\frac{3x}{8}+2x=\frac{1}{3}-12$

Now, the common denominator of the variable terms is . The common denominator of the constant values is . Thus, you can rewrite your equation:

$\frac{3x}{8}+\frac{16x}{8}=\frac{1}{3}-\frac{36}{3}$

Simplify:

$\frac{19x}{8}=-\frac{35}{3}$

Cross-multiply:

19x * 3 = -35*8

Simplify:

57x = -280

Finally, solve for :

$x = -\frac{280}{57}$

Report an Error

Example Question #18 : How To Evaluate A Fraction

Simplify the expression

$\frac{x^3y+3x^2y^2}{x^2-9y^2}$

Possible Answers:

$\frac{xy}{(x+3y)}$

$\frac{x^2y}{(x+3y)}$

$\frac{x^2y}{(x-3y)}$

$\frac{x}{(x-3y)}$

$\frac{x^2}{(x-3y)}$

Correct answer:

$\frac{x^2y}{(x-3y)}$

Explanation:

Begin by pulling out like factors in the numerator:

$\frac{x^3y+3x^2y^2}{x^2-9y^2}$

$\frac{x^2y(x+3y)}{x^2-9y^2}$

Now rewrite the denominator, since it is a difference of squares:

$\frac{x^2y(x+3y)}{(x+3y)(x-3y)}$

Cancelling like terms in the numerator and denominator leaves:

$\frac{x^2y}{(x-3y)}$

Report an Error

Example Question #262 : Gre Quantitative Reasoning

Reduce the following fraction

$\frac{a^2b^3c+ab^2c^2}{5a^2b}$

Possible Answers:

$\frac{ab(ab+c)}{5c}$

$\frac{5ab(ab+c)}{c}$

$\frac{ac(ab+c)}{5b}$

$\frac{bc(ab+c)}{5a}$

Correct answer:

$\frac{bc(ab+c)}{5a}$

Explanation:

To reduce this fraction we need to factor the numerator and find like terms in the denominator to cancel out.

The fraction

$\frac{a^2b^3c+ab^2c^2}{5a^2b}$

can be rewritten as

$\frac{ab^2c(ab+c)}{5a^2b}$

by factoring.

From here cancel like terms in the numerator and denominator:

$\frac{bc(ab+c)}{5a}$

Report an Error

Example Question #2 : Algebraic Fractions

A train travels at a constant rate of meters per second. How many kilometers does it travel in minutes? $(1\ km=1000\ m)$

Possible Answers:

Correct answer:

Explanation:

Set up the conversions as fractions and solve:

$\dpi{100} \small \frac{20m}{1sec}\times \frac{60sec^}{1min}\times \frac{1km}{1000m}\times \frac{10min}{1}$

Report an Error

Example Question #1 : How To Simplify A Fraction

Which quantity is greater?

Quantity A

$\frac{6}{33}+\frac{17}{24}$

Quantity B

$\frac{17}{32}+\frac{7}{25}$

Possible Answers:

The two quantities are equal.

Quantity B is greater.

Quantity A is greater.

The relationship cannot be determined from the information given.

Correct answer:

Quantity A is greater.

Explanation:

This can be solved using 2 methods.

The most time-efficient solution would recognize that $\frac{17}{24}$ is the largest value and nearly equals the sum the other fraction by itself.

The more time consuming method would be to convert each fraction to decimal form and calculate the sum of each quantity.

Quantity A: 0.1818+0.708=0.8898

Quantity B: 0.531+0.28=0.811

Report an Error

Example Question #2 : Algebraic Fractions

Simplify. $\frac{4x^{4}z^{3}}{2xz^{2}}$

Possible Answers:

$\frac{2x^{4}z^{3}}{xz}$

$2x^{4}z^{3}$

Can't be simplified

$4x^{3}z$

$2x^{3}z$

Correct answer:

$2x^{3}z$

Explanation:

To simplify exponents which are being divided, subtract the exponents on the bottom from exponents on the top. Remember that only exponents with the same bases can be simplified

Report an Error

Example Question #261 : Gre Quantitative Reasoning

Simplify:

$\frac{x^2-y^2}{x+y}$

Possible Answers:

x+y

x-y

2xy

$x-y,\ x+y$

Correct answer:

x-y

Explanation:

x² – y² can be also expressed as (x + y)(x – y).

Therefore, the fraction now can be re-written as (x + y)(x – y)/(x + y).

This simplifies to (x – y).

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Chicago, ISEE Tutors in Washington DC, English Tutors in New York City, LSAT Tutors in Seattle, Algebra Tutors in San Francisco-Bay Area, English Tutors in Phoenix, Computer Science Tutors in New York City, LSAT Tutors in New York City, Statistics Tutors in Seattle, ACT Tutors in Miami

Popular Courses & Classes

LSAT Courses & Classes in Houston, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Miami, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Houston, ISEE Courses & Classes in New York City, MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta, ACT Courses & Classes in New York City, SAT Courses & Classes in Houston

Popular Test Prep

LSAT Test Prep in Miami, ACT Test Prep in New York City, MCAT Test Prep in New York City, ISEE Test Prep in Seattle, GRE Test Prep in Denver, GMAT Test Prep in Philadelphia, GMAT Test Prep in Atlanta, MCAT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, MCAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #14 : How To Evaluate A Fraction

Example Question #41 : Algebraic Fractions

Example Question #13 : How To Evaluate A Fraction

Example Question #14 : How To Evaluate A Fraction

Example Question #18 : How To Evaluate A Fraction

Example Question #262 : Gre Quantitative Reasoning

Example Question #2 : Algebraic Fractions

Example Question #1 : How To Simplify A Fraction

Example Question #2 : Algebraic Fractions

Example Question #261 : Gre Quantitative Reasoning

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details