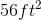Let's factor the square roots.

Then, multiply the numerator and the denominator by  to get rid of the radical in the denominator.

We can definitely eliminate some answer choices.  and  don't make sense because we have an irrational number. Next, let's multiply the numerator and denominator of  by . When we simplify radical fractions, we try to eliminate radicals, but here, we are going to go backwards.

, so  is the answer.

We don't want to have radicals in the denominator. To get rid of radicals, just multiply the numerator and the denominator by that radical.

Remember to distribute the radical in the numerator when multiplying.

This may be the answer; however, the numerator can be simplified. Let's factor out the squares. 

Finally, if we factor out a , we get:

Let's get rid of the radicals in the denominator of each individual fraction.

Then find the least common denominator of the fractions, which is , and multiply them so that they each have a denominator of .

We can definitely simplify the numerator in the right fraction by factoring out a perfect square of .

Finally, we can factor out a :

That's the final answer.

To get rid of the radical, we need to multiply by the conjugate. The conjugate uses the opposite sign and multiplying by it will let us rationalize the denominator in this problem. The goal is getting an expression of  in which we are taking the differences of two squares. 

This answer is the same as . Remember to distribute the negative sign.

To get rid of the radical, multiply top and bottom by .

Square both sides.

 is "opposite over adjacent," or . (This is because .)

Let's substitute  into the equation for  and multiply the numerator and the denominator by .

Now we can multiply the result by : 

 is the inverse of , or :

We can reduce the resulting  to : 

By multiplying top and bottom by , we can cancel out the  in the numerator:

The resulting fraction can be simplified:

To get rid of the radical, we need to multiply by the conjugate. The conjugate uses the opposite sign and multiplying by it will let us rationalize the denominator in this problem. The goal is getting an expression of  in which we are taking the differences of two squares.

You can "break apart" the fractional square root:

into:

Therefore, you can rewrite your equation as:

Now, multiply both sides by :

Now, you can square both sides of your equation and get:

The area of a square is length squared. In this case, that would be  which is equivalent to . At this point, you multiply the values underneath the square root, then simplify:

 .

The square root of a base squared is then just the base: 

Lastly, we apply the appropriate units, therefore the area of the courtyard is .